Лекции по системному анализу в чрезвычайных ситуациях. Часть 4
- Лекции по системному анализу в чрезвычайных ситуациях. Часть 4
- 1.1. Потоковые графы (графы состояний)
- 2. Моделирование с помощью орграфов
- 2.2. Взвешенные графы
- 2.3. Импульсные процессы в орграфах
- 2.4. Устойчивость и равновесие орграфа
- 2.5. Функциональные и гибридные и динамические орграфы
- 2.6. Орграфы с временными задержками
- 2.7. Управленческие решения при моделировании на орграфах
- Тема 2.2.5. Функциональные сети
- 2.2.52. Характеристики символов, используемых в диаграммах
- 2.2.5.
- ТЕМА 2.2.6. Сети Петри
- 2.2.6.2. Конечные разметки сети
- 2.2.6.3. Ограниченность сети Петри
- 2.2.6.4. Моделирование с помощью сетей Петри
- Тема 2.2.7. Основные принципы системного анализа и моделирования ущерба от техногенных аварий и катастроф
- 1.1.1. Первый этап
- 1.1.2. Второй этап.
- 1.1.3. Третий этап.
- 1.1.4. Четвертый этап
- 2. Классификация и анализ известных моделей и методов прогнозирования техногенного ущерба
- 2.2.7.2. Системные свойства новой реальности и риск
- 2.2.7.
- 2.2.7.
- Уровни управления риском
- Государственный уровень.
- Регионально‑отраслевой уровень.
- Сценарно‑объектовый уровень.
- Концептуальные модели риска
- 4.3. Анализ и управление профессиональным риском
При исследовании реальных систем важен учет времени реализации воздействия одного показателя на другой или о времени реакции одного показателя на изменения другого.
Простейший подход, который позволяет учесть временные задержки импульсного процесса — установка дополнительных промежуточных вершин. Например, если показатель j реагирует на изменение показателя i через одну временную единицу, а показатель l реагирует на изменение показателя i через три временных единицы, то орграф с временными задержками примет вид, который показан на рис. 7.
 |
Добавленные вершины l' и l" создают цепочку временных задержек передачи импульса от вершины i к вершине l. Очевидно, что весовые коэффициенты дуг (i, l') и (l', l") должны быть равны +1, а весовой коэффициент дуги (l", l) должен быть равен весовому коэффициенту дуги (i, l) исходного орграфа. Описанный подход возможен в случае целочисленности временных задержек, что имеет место в подавляющем большинстве моделей. Недостатком данного подхода является то, что количество вершин орграфа увеличивается, орграф становится громоздким и трудоемкость расчетов увеличивается. В то же время, все описанные выше способы анализа орграфа в таком варианте можно использовать без изменений.
 |
Второй способ учета временных задержек состоит в том, что каждой дуге орграфа ставятся в соответствие две характеристики: весовой коэффициент (знак, функция) и величина временной задержки. При таком способе учета можно использовать не только целочисленные временные задержки, можно принимать во внимание реализацию "мгновенного" изменения показателей, наряду с изменением показателей с временной задержкой. Под "мгновенным" изменением показателя следует понимать изменение показателя внутри рассматриваемого временного интервала, например, если интервал временной шкалы равен одному году, то все изменения показателей системы, которые изменяются внутри года (реакция показателя равна неделе, месяцу, кварталу) можно назвать "мгновенным". Для них время задержки равно нулю.
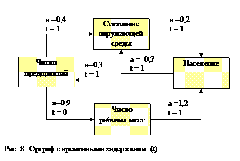
Пример такого орграфа приведен на рис.8.
Для решения задач с временными задержками, непосредственно указанными на дугах орграфа, следует использовать усложненный алгоритм, в котором будут учитываться временные задержки. При этом расчеты будут производиться до тех пор, пока не будут реализованы все "мгновенные" изменения показателей. Полученные результаты должны быть зафиксированы для данного момента времени и, исходя из зафиксированных значений, должны быть рассчитаны изменения показателей (сначала те, срок задержки которых истек, а затем те, у которых задержка равна нулю).
