Лекции для студентов

Лекции по системному анализу в чрезвычайных ситуациях. Часть 4

2. Конечные разметки сети

Одна из основных проблем в теории сетей Петри — задача о конечности функционирования сети (о достижении тупиковой разметки, “смертельные объятия” и т.д.).

Суть проблемы состоит в ответе на вопрос для данной конкретной сети — существует ли такая последовательность срабатывания переходов, которая приводит сеть к тупиковой разметке (т.е. разметке, при которой ни один переход не может сработать)?

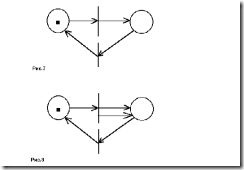
Если обратиться к рис.3 — очевидно, что последовательность P2,P2,P2,P2 (т.е. четыре подряд срабатывания перехода P2) делают дальнейшее срабатывание любого перехода в данной сети — невозможным. Желающие могут найти и другие последовательности срабатывания переходов, приводящих к такому результату.

Более того, анализ сети позволяет утверждать, что эта сеть всегда приходит к тупиковой разметке. Это математическое утверждение (теорема!) может быть строго доказано.

Заметим, что хотя рассматриваемая сеть обязательно останавливается, т.е. достигает тупиковой разметки, но сами эти тупиковые разметки могут быть различны.

Например, утверждение: “ сеть на рис.3 всегда останавливается, когда все фишки собраны в позиции V2” — справедливо.

А похожее утверждение: “ сеть на рис.3 всегда останавливается, причем все фишки собраны в позиции V2” — не верно.

Свойство достижения конечной разметки присуще далеко не всем сетям. Например, на рис.4 приведен пример сети всегда приходящей к тупиковой разметке, на рис.5 — сеть никогда не “попадает в тупик”, на рис. 6 — сеть, которая может остановиться, а может и нет.