Лекции по системному анализу в чрезвычайных ситуациях. Часть 4
- Лекции по системному анализу в чрезвычайных ситуациях. Часть 4
- 1.1. Потоковые графы (графы состояний)
- 2. Моделирование с помощью орграфов
- 2.2. Взвешенные графы
- 2.3. Импульсные процессы в орграфах
- 2.4. Устойчивость и равновесие орграфа
- 2.5. Функциональные и гибридные и динамические орграфы
- 2.6. Орграфы с временными задержками
- 2.7. Управленческие решения при моделировании на орграфах
- Тема 2.2.5. Функциональные сети
- 2.2.52. Характеристики символов, используемых в диаграммах
- 2.2.5.
- ТЕМА 2.2.6. Сети Петри
- 2.2.6.2. Конечные разметки сети
- 2.2.6.3. Ограниченность сети Петри
- 2.2.6.4. Моделирование с помощью сетей Петри
- Тема 2.2.7. Основные принципы системного анализа и моделирования ущерба от техногенных аварий и катастроф
- 1.1.1. Первый этап
- 1.1.2. Второй этап.
- 1.1.3. Третий этап.
- 1.1.4. Четвертый этап
- 2. Классификация и анализ известных моделей и методов прогнозирования техногенного ущерба
- 2.2.7.2. Системные свойства новой реальности и риск
- 2.2.7.
- 2.2.7.
- Уровни управления риском
- Государственный уровень.
- Регионально‑отраслевой уровень.
- Сценарно‑объектовый уровень.
- Концептуальные модели риска
- 4.3. Анализ и управление профессиональным риском
Устойчивость импульсных процессов подразделяется на два типа: импульсная и абсолютная.
Взвешенный орграф называется импульсно устойчивым, если для каждой его вершины последовательность 
ограничена, т.е. найдется такое положительное число Pj (S), что | Pj (S) | £ Pj для всех S = 0, 1, 2 …. .
Взвешенный орграф называется абсолютно устойчивым, если для каждой его вершины последовательность 
ограничена, т.е. найдется такое положительное число Vj (S), что | Vj (S)| £ Vj для всех S = 0, 1, 2 …. .
Применительно к равновесию орграфа также можно говорить о двух типах равновесия.
Взвешенный граф находится в состоянии импульсного равновесия, если Pj (S) = Pjдля всех j Î J и S = S’, S’+1, S’+2, ….
Взвешенный граф находится в состоянии абсолютного равновесия, если Vj (S) = Vjдля всех j Î J и S = S’, S’+1, S’+2, ….
Примеры импульсных и абсолютных устойчивости и равновесия приведены на рис. 7.
 |
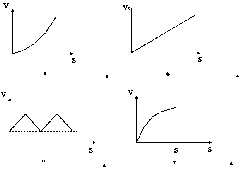Рис.7
а) орграф импульсно и абсолютно неустойчив;
б) орграф импульсно устойчив, но абсолютной устойчивости нет;
в) орграф устойчив как импульсно, так и абсолютно, однако ни импульсное ни абсолютное равновесие на отрезке S …. ¥ не достигнуто;
г) импульсное ни абсолютное равновесие достигнуто на отрезке S’ …. ¥
