Лекции для студентов

Лекции по системному анализу в чрезвычайных ситуациях. Часть 4

ТЕМА 2.2.6.  Сети Петри

1. Основные понятия

2. Конечные разметки сети

3. Ограниченности сети Петри

4. Моделирование с помощью сетей Петри

1. Основные понятия

Рис.1

Графы специального вида, получившие в дальнейшем название “Сети Петри” были впервые введены Карлом Петри в 60-х годах. В следующем десятилетии начался “бум” разработок в этом направлении. В настоящее время поисковые машины Интернет дают несколько десятков тысяч ссылок на использование этого термина.

Популярность сетей Петри вызвана удачным представлением различных типов объектов, присутствующих во многих моделируемых системах и “событийным” подходом к моделированию. Прекрасное изложение теории сетей Петри можно найти на русском языке в [1] и [2]. Формальное определение сетей Петри будет приведено ниже. Здесь же дать простое представление об этом математическом инструменте.

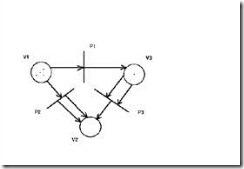
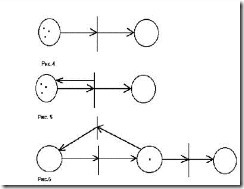
Сеть Петри определяется как двудольный граф. Т.е. все вершины графа относятся к одному из двух классов — позициям и переходам. Позиции изображаются окружностями, переходы — отрезками прямой. Дуги в сетях Петри — направленные. Причем каждая дуга связывает вершины только разных классов.

Либо начало дуги совпадает с позицией и тогда конец этой дуги совпадает с переходом, либо наоборот.

Рис.2

На рис.1 приведены примеры, соответствующие этому ограничению, на рис.2 — недопустимые примеры.

Оригинальным понятием теории сетей Петри является понятие “фишка”. Фишки изображаются точками, расположенными внутри позиций. Таким образом, каждой позиции сети ставится в соответствие натуральное число, указывающее количество фишек в данной позиция. Это число называют разметкой позиции, а совокупность таких чисел для всех позиций сети называют разметкой сети. Замечу, что позиция может и не содержать фишек, т.е. иметь нулевую разметку.

Пример сети с разметкой приведен на рис.3.

Другое оригинальное понятие сети Петри — “срабатывание” переходов.

Рис.3

Назовем входными позициями некоторого конкретного перехода — те позиции, из которых исходят дуги, входящие в данный переход. Соответственно, выходными позициями назовем позиции, в которые входят дуги, исходящие из данного перехода.

Например, на рис.3 для перехода P1 входная позиция V1- выходная -V3.

Срабатывание перехода состоит в изъятии фишек из каждой входной позиции и помещении их в каждую выходную позицию. Причем, количество фишек, изымаемых из конкретной позиции, или помещаемых в конкретную позицию равно количеству дуг, соединяющих срабатывающий переход с данной конкретной позицией.

Например, переход P1 на рис.3 при срабатывании изымает из позиции V1 одну фишку и увеличивает количество фишек в позиции V3 на одну.

Переход P2 изымает одну фишку из позиции V1 и помещает в позицию V2 две фишки.

Теперь естественно вводится условие срабатывания перехода. Переход срабатывает, если количество фишек в каждой входной позиции перехода не меньше количества дуг, соединяющих эту позицию с переходом.

Например, на рис.3. переход P3 не может сработать, ибо в позиции V3 находится только одна фишка, а дуг, связывающих V3 и P3 — две.

Как только введено понятие “срабатывание” перехода — появляется возможность говорить о функционировании сети и моделировании процессов, этапы которых связаны между собой причинно-следственной связью.

В самом деле, на рис.3 изображена сеть, в которой переход P3 не может сработать. Но если сработает переход P1, то количество фишек в позиции V3 — увеличится. Теперь P3 — сработает.

Разметку сети до срабатывания любого перехода называют начальной или стартовой разметкой. Затем срабатывает тот или иной переход. При этом разметка сети меняется. Возможно, что в результате этого изменения некоторый переход потеряет возможность срабатывать, или наоборот — приобретет ее. Последовательное срабатывание переходов и соответствующее изменение разметки сети называют процессом функционирования сети.

Завершение процесса функционирования приводит сеть к разметке, называемой конечной.

Собственно говоря, предметом теоретического исследования сетей Петри и является процесс их функционирования, т.е. возможные последовательности срабатывания переходов и свойства получаемых при этом разметок сети. И, как обычно в математике, такие исследования формулируются, как правило, в виде утверждений двух основных типов — утверждение о существовании и утверждения об обязательности.