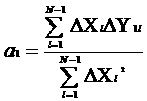Лекции для студентов

Лекции по системному анализу в чрезвычайных ситуациях. Часть 4

2.2. Взвешенные графы

Свойства взвешенного орграфа весьма чувствительны к весам, которые присваиваются дугам. Поэтому значение весов следует устанавливать с возможно большей точностью.

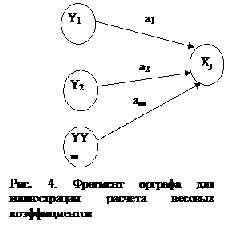Определение весов дуг орграфа. может быть проведено так же, как и знаков, на основе логики и экспертных оценок. В случае, когда имеется статистическая информация, весовые коэффициенты могут быть установлены на основе обработки этой информации. Поскольку наблюдаемые изменения показателей происходят одновременно под действием всей совокупности взаимосвязей, то следует провести разделение изменения показателя под действием каждой, отдельно действующей на него, дуги. Иначе говоря, надо обеспечить определение весовых коэффициентов в соответствии с принципом "при прочих равных условиях". Для этого надо решить оптимизационную задачу обработки статистических данных.

Если известно N значений изменений показателей X_j в системе и эти изменения происходят практически мгновенно, то исходя из известной статистической информации, представленной в табл. 1 для фрагмента орграфа (рис. 4), следует решить задачу:

,

где  — l-е приращение значения j-го показателя при l-м приращении значения i-го показателя , воздействующего на исследуемый показатель X_j ; , N-1;

Табл. 1. Статистическая информация для расчета весовых коэффициентов

Показатели	Значения показателей для наблюдений
l=1	l=2	l=3	…	l=N
Исследуемый показатель Xj	Xj1	Xj2	Xj3		XjN
Воздействующие показатели
Y1	Y11	Y12	Y13		Y1N
Y2	Y21	Y22	Y23		Y2N
…
Ym	Ym1	Ym2	Ym3		YmN

Приведенная оптимизационная задача — минимизация суммы квадрата разности действительного значения показателя и его расчетного значения, получаемого на базе суммы произведений значений влияющих на него показателей и весовых коэффициентов. Данный подход — применение метода наименьших квадратов для расчета весовых коэффициентов орграфа. Его реализация проста: достаточно найти частные производные минимизируемой функции по искомым весовым коэффициентам, приравнять их к нулю и решить полученную систему линейных уравнений. В случае, если т = 1 коэффициент определяется по формуле (для простоты записи индекс j для исследуемого показателя далее опускается):

,

если же т = 2, то требуется решить линейную систему из двух уравнений с двумя неизвестными:

a₁∆y_1l² +a₂∆y_1l×∆y_2l = а₁∆x_l ∆y_1l

a₁∆y_1l ∆y_2l+a₂∆y_2l² = ∆x_l∆y_2l

В случаях, когда статистическая информация отсутствует, весовые коэффициенты можно определить на основе экспертных оценок, отдавая себе отчет в том, что точность модели в этом случае существенно ниже.

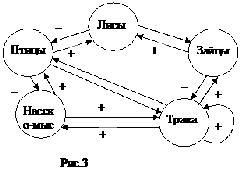
Для примера рассмотрим орграф модели рыночного механизма установления цен и выпуска продукции (рис. 5). Орграф имеет контуры 1-2-1, 1-3-4-1, 1-2-3-4-1.

Из теории графов известно, что контуры могут как усиливать в конечном итоге отклонения переменных (контуры положительной обратной связи), так и уменьшать их (контуры отрицательной обратной связи). Контур усиливает отклонение тогда, и только тогда, когда он содержит четное число отрицательных дуг. Контур противодействует отклонению тогда и только тогда, когда он содержит нечетное число отрицательных дуг.

Если большинство контуров составляют контуры, усиливающие отклонение, то начальные изменения могут превышать изменения в результате их непосредственного воздействия. таким образом, наличие многих контуров, усиливающих отклонение, предполагает неустойчивость.

Рис. 5