Лекции для студентов

Лекция по автоматике

Апериодическое (инерционное) звено первого порядка

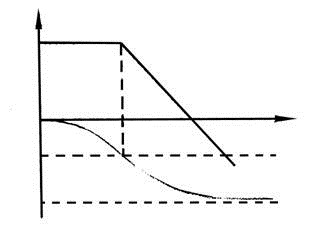
Апериодическим называется такое звено, у которого выходная величина после подачи на вход ступенчатого воздействия изменяется монотонно, достигая некоторого установившегося значения.

                                                                 1.70

Дифференциальное уравнение в операторной форме

                                                               1.71

Апериодические звенья первого порядка наиболее часто применяются в практике автоматического регулирования.

 

 

Примеры звеньев:

1)нагрев тела

 

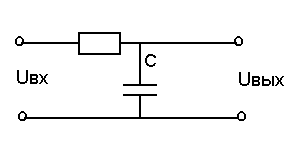
2)RC-цепь

 

 

 

 

 

Передаточная функция

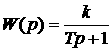                                                                  1.72

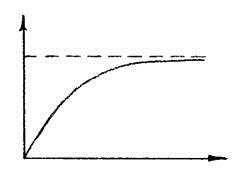
Переходная функция

 

                                                   1.73

 

 

Функция веса

 

 

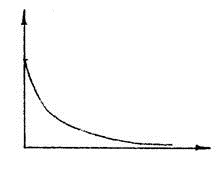                                                                       1.74

 

 

Для рассматриваемого звена временной характеристикой может служить решение дифференциального уравнения (1.70).

                                                   1.75

Из выражения (1.75) можно перейти к выражению (1.73), если на вход подать ступенчатое воздействие, а начальные координаты принять равные нулю.

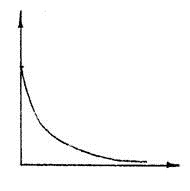
Теоретически, переходный процесс у звеньев рассматриваемого типа, длится бесконечно долго. Практически же, для апериодического звена, переходный процесс может быть завершенным, если выходная величина достигает значения 0,95-0,99 от установившегося. Такой промежуток времени определяется значениями (3Т...5Т).

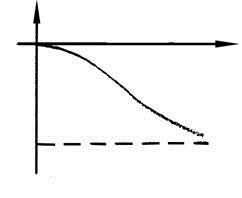
Частотные характеристики

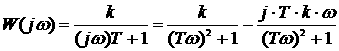                                                1.76

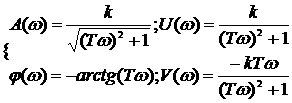                                                           1.77

Вид частотных характеристик

     АФХ                                      АЧХ                                       ФЧХ

 

 

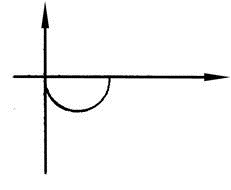Выражение для ЛАЧХ

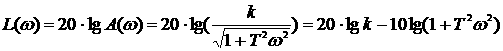                  1.78

Выражение для аналитической ЛАЧХ

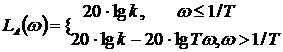                                                  1.79

Вид логарифмических характеристик