Лекции для студентов

Лекция по автоматике

Понятие о типовых входных сигналах (воздействиях).

Оценку динамических свойств САУ, т.е. их поведение в переходных режимах можно выполнить различными методами. Решение динамического уравнения, которым описывается звено или система при заданных  начальных условиях также отображает их динамику. Оно представляет переходный процесс звена или системы во времени. Для сравнения различных динамических свойств различных элементов рассматривают их переходные процессы, при нулевых начальных условиях и типовых входных воздействий.

Начальные условия — это значение выходной величины, а также всех ее производных в момент времени равное нулю, при условии, что до этого времени внешнее воздействие отсутствовали. Эти начальные условия являются нулевыми, т.к. y(t₀)=y´(0)=…=yⁿ(0)=0.

В качестве типовых входных воздействий принимают определенные формы воздействий, наиболее удобные с точки зрения их математического описания, практической реализации и описания реакции звена на эти воздействия. Иными словами, входное воздействие должно быть простым, не затрудняющим решение уравнения и соответствовать самому тяжелому режиму работы системы из числа встречающихся при ее эксплуатации.

Различают типовые входные воздействия, описываемые следующими функциями:

1.       ступенчатой

2.       импульсной

3.       гармонической

Первые две функции представляют собой временные характеристики звена или системы, а последняя — частотные характеристики.

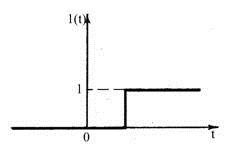
1.       Единичное ступенчатое воздействие.

Оно описывается единичной ступенчатой функцией:

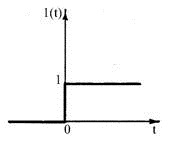а) "Включение" 1(t)

 

 

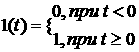   1.24

 

 

 

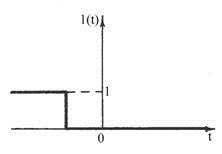
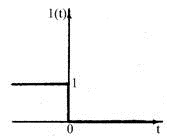б) "Отключение" 1(t)

 

 

 

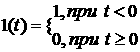   1.25

 

в) "Включение с задержкой"

 

 

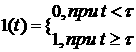    1.26

 

 

г) "Отключение с задержкой"

 

 

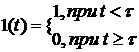   1.27

 

 

 

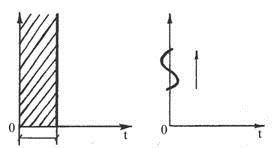
2.       Импульсное воздействие (единичный импульс).

Импульсное воздействие описывается единичной импульсной функцией d — Дирака (d(t)) является математической идеализацией короткого импульса, площадь которого равна единице, при его длительности равной нулю и амплитуде равной +¥:

 

 

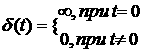  1.28

 

 

Свойство d(t): площадь этой функции равна 1:

                                                                            1.29

                                                                         1.30

3.       Гармоническое воздействие.

Такое воздействие описывается гармонической функцией вида:

                                                                            1.31

Если к звену или системе приложено воздействие, отличающегося от ступенчатого или импульсного, то его представляют в виде суммы последовательных импульсных или ступенчатых воздействий на звено или систему. Реакция звена или системы на такое воздействие может быть получено с использованием интеграла Дюамеля.