Лекция по автоматике

Операторная форма записи дифференциального уравнения. Передаточная функция.

Динамика функциональных элементов и систем управления описывается дифференциальным уравнением, которое в общем виде можно записать как

         1.15

Необходимо, чтобы n >m, для работы системы. Описание существенно упрощается если от дифференциального уравнения перейти к операторной форме. Для этого необходимо операцию дифференцирования заменить на оператор дифференцирования

р₁ — оператор дифференцирования

В результате такой замены мы получили алгебраическое уравнение

             1.16

Если в уравнении (1.15) вместо функции времени у(t) и х(t) ввести функции х(р) и у(р) комплексного переменного р=α±jβ , поставив условием что записанные функции связаны отношением

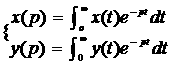                                                      1.17

то оказывается что дифференциальное уравнение, содержащие х(t) и у(t) равносильно алгебраическому уравнению вида

      1.18

Следует отметить, что трансформация дифференциального уравнения в представленное алгебраическое возможно только при нулевых начальных условиях. И это преобразование в математике называют преобразованием Лапласа. Функции х(р) и у(р) называют изображениями функций х(t) и у(t), а сами функции х(t) и у(t) называют оригиналами функций х(р) и у(р).

Переход от искомой функции у(t) к изображению у(р) называют прямым преобразованием Лапласа, и обозначают

                                                                    1.19

Переход же от изображения у(р) к оригиналу у(t) называют обратным преобразованием Лапласа

                                                                 1.20

Из сравнения уравнений (1.18) и (1.16) видно, что обе формы записи совпадают, из чего следует, что оператор дифференцирования отождествляется с комплексной переменной р при нулевых начальных условиях.

Использование операторной формы представления уравнений позволяет избежать решения дифференциальных уравнений путем решения системы алгебраических уравнений. Нахождение оригиналов по изображениям можно провести используя либо справочные таблицы, либо формулу разложения.

Взяв за основу формулу (1.18) можно найти отношение

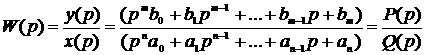                          1.21

Передаточной функцией W(р) называют отношение изображения по Лапласу выходной величины к изображению входной величины при нулевых начальных условиях.

Из уравнения (1.21) можно записать

                                                               1.22

Многочлен, фигурирующий в знаменателе передаточной функции называется характеристическим многочленом, а в случае приравнивания его у нулю уравнение называется характеристическим.

                                            1.23

Корни характеристического уравнения называют полюсами передаточной функции. Корни многочлена, расположенного в числителе передаточной функции, называют нулями передаточной функции.