Автоматика
Лекция по автоматике
Лекция по автоматике
Автоматика — отрасль науки и техники, которая охватывает теорию автоматического управления, а также принципы построения автоматических систем и технические средства, для реализации этих систем.
Автоматизация — применение технических средств, экономическо-математических методов и систем управления, освобождающих человека полностью или частично от непосредственного участия в процессе получения, преобразования, передачи и использования энергии, материалов или информации.
С/х производству присущи свои специфические особе6нности, которые следует учитывать при автоматизации:
1. цикличный, прерывистый характер производства
2. невозможность сбоев;
3. надежность используемых средств автоматизации;
4. невозможность увеличить выход продукции, уменьшив время и число циклов;
5. наличие существенных и продолжительных вибраций в мобильной технике;
6. большое количество объектов с агрессивными, влажными и запыленными средами;
7. рассосредоточенность с/х машин и установок по огромным площадям, а также удаленность их от ремонтных баз.
В зависимости от функций, выполняемых специальными автоматическими устройствами различают следующие виды автоматизации:
1. Автоматический контроль (автоматическая сигнализация, автоматические измерения, автоматическая сортировка, автоматический сбор информации);
2. Автоматическая защита (релейная защита, автоблокировка);
3. Дистанционное управление (дистанционное управление, телемеханика);
4. Автоматическое регулирование и автоматическое управление (САУ, САР);
5. Автоматизированное управление (автоматизированные системы управления технологическими процессами, системы автоматизированного проектирования, автоматизированные системы сбора экономической информации)
По степени автоматизации производственных процессов различают:
1. частичная автоматизация;
2. комплексная автоматизация;
3. полная автоматизация.
Чем качественней автоматизация, тем меньше себестоимость продукции, тем больше ее выпуск и и выше доход.
Основные понятия, определения, термины
Любой технологический процесс характеризуется физическими величинами, называемыми показателями процесса. Для одних процессов показатели могут быть постоянными, для других же допускается их изменение в заданных пределах по определенному закону.
Совокупность предписаний, ведущих к правильному выполнению технологического процесса в каком-либо устройстве или ряде устройств, выполняющий один и тот же технологический процесс называется алгоритмом (законом) функционирования устройства или системы.
Устройства или совокупность устройств, осуществляющих тот или иной технологический процесс, которые нуждаются в оказании специально организованных командах извне для выполнения алгоритма функционирования называются объектом управления (ОУ).
Каждый ОУ должен иметь устройство, называемое управляющим органом, при изменении положения или состояния которого, показатели процесса будут изменяться в заданных пределах или заданных направлениях. Через управляющий орган в ОУ поступают воздействия, которые позволяют осуществлять заданный алгоритм функционирования.
Совокупность предписаний, определяющая характер воздействий извне на управляемый объект с целью управления или заданного (предписанного) алгоритма функционирования называется алгоритмом управления. Физические показатели процесса или объекта, которые преднамеренно изменяются, или сохраняются неизменными в процессе управления называются управляемыми (регулируемыми) величинами или координатами. Обычно управляемые величины в объектах управления характеризуют качественные показатели процесса. Поэтому управлять объектом — это значит создавать условия, при которых качественные показатели изменялись бы по требуемому закону с определенной точностью, независимо от действующих на объект внешних условий.
Управление – это преднамеренное воздействие на объект управления, обеспечивающее достижение определенных самим технологическим процессом целей.
Если управление осуществляется без непосредственного участия человека, то оно называется автоматическим, а если с участием, то ручным.
Автоматическим управляющим устройством (АУУ) называют техническое устройство, осуществляющее воздействие на объект управления, в соответствии с заложенным в нем алгоритмом управления. АУУ воздействует на ОУ через орган управления. Совокупность ОУ и АУУ взаимодействующих между собой, в соответствии с алгоритмом управления называют системой автоматического управления (САУ).
Из всех операций управления ТП объединенных определением САУ наибольший интерес для практических целей представляют операции по поддержанию или изменению показателей процесса.
Такого рода операций получили название процесса регулирования. Техническое устройство, предназначенное для автоматического поддержания постоянного значения показателей процесса регулирования или изменения этих показателей по какому-либо требуемому закону называют автоматическим регулятором (АР). Совокупность ОР с АР называют системой автоматического регулирования (САР).
Понятие о воздействиях и сигналах
В процессе работы САУ в целом, а также, если рассматривать отдельные ее части, то либо система, либо ее составляющие, испытывают на себе воздействие различных факторов.
Воздействием в автоматике называют взаимодействие между автоматической системой и внешней средой, или одной ее части и другой, при котором в самой система происходят изменения. Соответственно различают внешние и внутренние воздействия.
1. Внутренними воздействиями называют такие, которые передаются от одной части системы на другую, образуя последовательную цепь воздействий, обеспечивающих протекание ТП с заданными показателями. Также воздействия называют управляющими и обозначают в функции времени как U(t).
2. Внешние воздействия разделяют на 2 вида:
2.1 Такие, которые необходимы для нормального протекания технологического процесса. Их подают на вход системы намеренно в соответствии с алгоритмом функционирования, обозначают x(t) или xз(t) и соответственно при этом называют задающими или предписанными.
2.2 Такие, которые поступают непосредственно в систему или объект из внешней среды, т.е. из окружающего пространства, или от технических средств и устройств, не принадлежащих рассматриваемой сичстеме. Также воздействие носят незапланированный, зачастую случайный характер, обозначаются как f(t) и называются возмущающими воздействиями или возмущениями.
Возмущения делятся на нагрузку и помеху.
Нагрузка — возмущение, поступающее в систему, помимо управляющего воздействия, влияющее на переменные состояния и параметры, которые характеризуют динамические свойства ОУ.
Помеха — возмущение, искажающее поступающую в управляющее устройство информацию о нагрузке, о состоянии и динамических свойствах ОУ, а также влияющее на переменное состояние и параметры управляющего устройства (УУ). Возмущения могут быть контролируемыми и не контролируемыми, детерминированными (заданными функцией времени) и стохастическими (случайными), основными и второстепенными.
Под влиянием заданного значения x(t) в системе автоматического управления происходят различные количественные и качественные изменения, в результате чего управляемые или регулируемые величины, обозначаемые как y(t) приобретают заданные значения, или получают требуемый характер изменения.
Значение управляемой величины, предусмотренное алгоритмом функционироваия называется предписанным, а измеренное, т.е. фактическое значение — действительным.
Кроме того, задающее значение x(t) называют входным, а управляемую величину y(t) — выходной.
Изобразим простейший алгоритм регулирования температуры внутри нагревательной камеры.
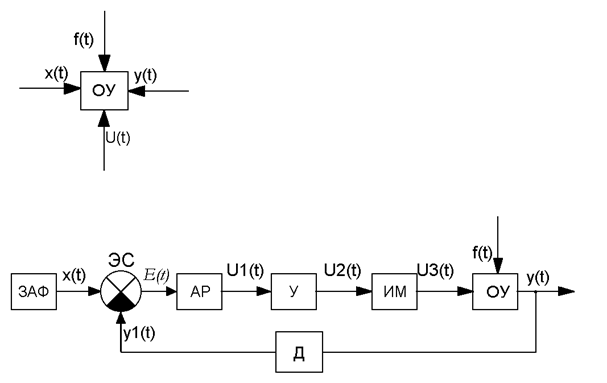
Управлять объектом – это значит вырабатывать управляющее воздействие U(t) с таким расчетом, чтобы управляемая или регулируемая величина y(t) изменялась по заданному закону и с требуемой точностью независимо от влияния на объект, а возмущающего воздействия f(t).
Любая САУ может быть представлена как взаимодействие автоматического управляющего устройства или автоматического регулятора и объекта управления.
Более просто можно показать влияние сигналов и воздействий, если рассмотреть только ОУ:
Если в системе одна управляемая величина, то такая система называется одноконтурной, а если этих величин несколько, причем изменение одной влияет на другие, то такую систему называют многоконтурной.
Обратные связи и их назначение
Из анализа процесса управления видно, что в организации самого процесса большую и решающую роль играет получение информации о результатах управления. При получении такой информации решение об управляющих действиях существенно зависит от результатов управления. Иными словами — первичный элемент, управляющий действием, зависит от вторичного элемента, вызываемый управляющим действием, т.е. причина, вызывающая изменение состояния ОУ находится в зависимости от того, какой результат она вызовет. Такая связь причины и следствия называется причинно-следственной или обратной связью.
Обратная связь — это связь по которой информация о состоянии ОУ (контролирующее воздействие, соответствующее действительному значению управляемой величины) передается с выхода системы на ее вход.
Обратные связи подразделяются:
1. отрицательные и положительные;
2. жесткие и гибкие;
3. местные и главные.
Если воздействие обратной связи, поступающее на вход системы по знаку совпадает со знаком задающего воздействия, то ее называют положительной, в противном случае связь определяют как отрицательную.
В автоматике ООС и ПОС принято указывать, начиная с функциональных схем следующим образом.
Если передаваемое воздействие зависит только от выходной величины и не зависит от времени — связь считают жесткой. Жесткие обратные связи, действуют как в установленном, так и в переходном режиме.
Обратная связь, оказывающая влияние на работу системы только в переходном процессе (режиме) называется гибкой. Такие связи реагируют на приращение воздействий, поступающих на вход системы. Те из них, что реагируют на производные от воздействий называются дифференцирующими гибкими связями, а те, которые реагируют на интегралы от воздействий, называются интегрирующими обратными гибкими связями.
Если обратная связь соединяет выход системы с ее входом, то ее называют главной, а остальные же обратные связи называют местными.
Такие связи служат для улучшения регулировочных свойств отдельных элементов или их групп, соединяя выход элемента, или группы с соответствующим входом. Такие связи, кроме названия местные именуют корректирующими. Местные и главные связи могут быть как жесткими, так и гибкими.
В случае размыкания главной обратной связи система работающая по замкнутому циклу переходит в режим работы по разомкнутому циклу. В случае же размыкания местной обратной связи система продолжает работать по заложенному в нее циклу.
Управление по разомкнутому и замкнутому циклам
Поддержание управляемой величины в определенных пределах или изменение ее по заданному закону в процессе работы системы может быть выполнена как по разомкнутому, так и по замкнутому циклам.
1. Разомкнутый цикл управления
Воздействие x(t), поступающее на автоматическое устройство управления или автоматический регулятор от задатчика алгоритма функционирования не является функцией результата этого воздействия на объект управления — оно задается. Определенному значению x(t) будет соответствовать определенное текущее значение y(t), если возмущение f(t) не изменяется во времени (f(t)=const).
По сути, разомкнутая система представляет собой передаточную цель, в которой x(t) после определенной обработки АУУ или АР преобразуется во внутренние воздействия U1(t) и U2(t) и передается ОУ, но при этом нет обратного воздействия на АУУ или АР.
Покажем пример такого цикла функционирования, рассмотрев систему регулирования скоростью вращения ДПТ.
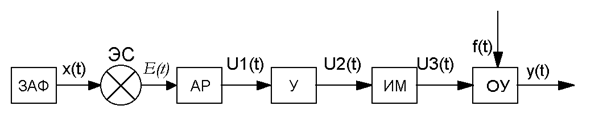
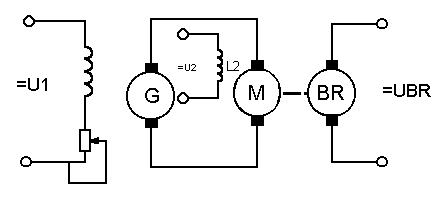
2. Замкнутый цикл управления
По замкнутому циклу САУ работает если соединить ее выход со входом АР или АУУ так, чтобы на него все время поступало 2 воздействия — с задатчика и с выхода ОУ, т.е. в рассматриваемой системе существует воздействие не только АУУ или АР на ОУ, но и ОУ на АУУ или АР.
Покажем пример работы системы АУ скорости вращения ДПТ, работающей по замкнутому циклу.
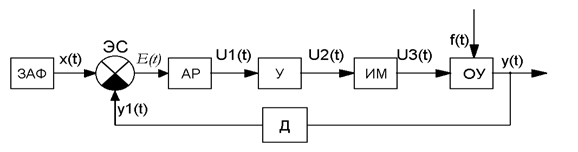
Классификация систем автоматического управления
Большое разнообразие, используемых в технике систем АУ требует применение различных признаков классификации таких систем. Рассмотрим классификации:
1. По характеру алгоритма функционирования:
1.1 Система стабилизации.
Они поддерживают требуемое значение управляемой величины с заданной точностью. В этих системах задающих воздействие x(t)=const. Стабилизация выходной величины ОУ осуществляет автоматический регулятор.
1.2 Системы программного управления.
Они предназначаются для изменения управляемой величины по определенному предписанию программе, которое составляется заранее на основании требований технического процесса. Сама программа задается при помощи задатчика и представляет собой последовательность команд в соответствии с алгоритмом функционирования ОУ.
1.3 Следящие автоматические системы.
Они предназначаются для изменения управляемой величины по закону, заранее неизвестной функции времени. В таких системах применяется своя терминология:
· входная величина — ведущая
· выходная — ведомая
· окончание процесса — отработка и т.д.
2. По способности САУ к самоприспосабливаемости.
САУ в составе которых имеются дополнительное автоматическое управление, изменяющее алгоритм функционирования основного АРУ, таким образом, чтобы система в целом осуществляла ЗАФ, называется самоприспосабливающимся. Такие системы обладают свойством адаптации, т.е. свойством автоматического приспособления к непредвиденным изменениям параметров объекта регулирующих устройств и внешней среды.
2.1 Системы экстремального управления.
Они обеспечивают отыскание и поддержания таких регулирующих воздействий на ОУ, при которых управляемая величина достигает наибольшего или наименьшего значения. Они действуют по принципу "поиска", т.е. обязательно с подачей поисковых сигналов. По получению отклика на сигнал поиска определяется знак и значение dy/du или dy/dt и затем определяется экстремум.
2.2 Системы с перестраивающимися устройствами.
Эти системы, у которых параметры или их структура автоматики изменяется в зависимости от управляющих и возмущающих воздействий или переменных параметров объекта.
2.3 Аналитические самонастраивающиеся системы.
Это системы, у которых их перестройка осуществляется на основе аналитического определения их динамических характеристик. В состав этих систем обязательно входит вычислительные машины.
3 По характеру управления во времени.
3.1. Непрерывные САУ.
3.2. Дискретные САУ (импульсные системы, релейные и позиционные системы)
4. По математическому описанию.
4.1 Линейные САУ.
4.2 Нелинейные САУ.
5 По числу управляемых величин.
5.1 Одномерные системы.
5.2 Многомерные системы.
6 По принципу действия.
6.1 Системы прямого действия. Это системы в которых чувствительный элемент (датчик) действует непосредственно на управляемый орган.
6.2 Системы непрямого действия. Это системы у которых после чувствительного элемента установлены усилители и сервоприводы.
7 По виду зависимости между управляемой величиной и нагрузкой на ОУ.
7.1 Системы статического регулирования.
Статическая система — это система, в которой при возмущающем или задающем воздействии, стремящемся к постоянной величине, отклонение управляемой величины также стремится к постоянной величине зависящей от этого воздействия. Для реализации такой системы используют статический регулятор. Такие системы функционируют с некоторым отклонением — статической ошибкой или статизмом системы.
7.2 Система астатического регулирования.
Астатическая система — это система, в которой при возмущении или задании отклонения управляемой величины в установившемся режиме, при постоянном значении, возмущения или задания равно нулю. Функционирует такая система при помощи астатических регуляторов, значения коэффициента астатизма равны нулю.
Основные законы управления
Под законом управления в автоматике понимают математическую зависимость, по которой управляющее устройство или регулятор воздействует на объект управления. В автоматике будут рассмотрены только простейшие законы управления, в которых управляющие воздействия линейно зависят от отклонения от его интеграла и дифференциала.
1. Пропорциональный закон (П-закон).
Это закон реализуется пропорциональным регулятором (П-регулятором). П-регулятор реализует статическое регулирование. Рассматриваемы законы регулирования реализуются при помощи автоматических устройств или регуляторов, на вход которых подается отклонение управляемой величины (сигнал рассогласования), а на выходе формируется управляющее воздействие.
Уравнение П-закона имеет вид:
1.1
где кр - коэффициент передачи регулятора (коэффициент усиления регулятора).
U(t) — управляющее воздействие (формируется на выходе регулятора).
e(t) — отклонение управляемой (регулируемой) величины от заданного значения (поступает на вход регулятора).
2. Интегральный закон (И-закон).
Рассматриваемый закон реализуется И-регулятором в процессе астатического регулирования. Уравнение закона:
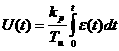1.2
1.3
где кр — коэффициент передачи И-регулятора
Ти — постоянная времени интегрирования И-регулятора
3. Пропорционально-интегральный закон (ПИ-закон)
Данный закон регулируется ПИ-регулятором, т.е. происходит пропорциональное регулирование с интегральной коррекцией. Регулирование в данном случае является астатическим. Выражение ПИ-закона:
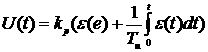1.4
1.5
4. Пропорционально-интегрально-дифференциальный закон (ПИД-закон).
Данный закон регулируется ПИД-регулятором, а само регулирование является астатическим. Выражение этого закона:
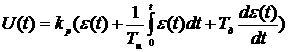1 1.6
где Ти; Тд — постоянные времени интегрирования и дифференцирования ПИД-регулятора.
Графики поведения управления управляемой величины во времени, при участии в системе различных регуляторов. Рассматриваемый ОУ обладает свойством саморегулирования.
1 — система самовыравнивания без регулирования.
2 — система с П-регулятором.
3 — система с И-регулятором.
4 — система с ПИ-регулятором.
5 — система с ПИД-регулятором.
Принципы действия систем автоматического управления.
При проектировании САУ решают, как наиболее простым и технико-обоснованным способом получить и передать необходимый объем информации. Для этого исследуют принципы построения систем. Основными принципами построения систем являются:
1. принцип разомкнутого управления.
2. принцип управления по отклонению.
3. принцип компенсации.
4. принцип комбинированного управления.
1. Принцип разомкнутого управления.
Данный принцип заключается в том, что алгоритм управления строится только на основе алгоритма функционирования путем предварительного выбора законов, определяющее действие управляемого устройства или регулятора с учетом свойств управляемого объекта. Алгоритм функционирования может задаваться отдельным устройством (ЗАФ) или может быть заложен в конструкцию управляющего устройства или регулятора.
Примером данного принципа может служить пример разомкнутого цикла управления.
2. Принцип управления по отклонению.
Этот принцип также именуется принципом Уатта-Ползунова. Рассматриваемый принцип управления основан на том, что управляющее воздействие в автоматическом устройстве управления или регуляторе вырабатывается с учетом информации об отклонении.
Управление величины от заданного значения. Чтобы реализовать этот принцип, в автоматическом устройстве управления или в автоматическом регуляторе должно происходить сравнение действительного значения y(t) с заданным или предписанным x(t), и в зависимости от результатов полученного сравнения, формируется управляющее воздействие. Примером реализации данного принципа может служить пример замкнутого цикла функционирования.
3. Принцип управления по возмущению (принцип компенсации возмущения).
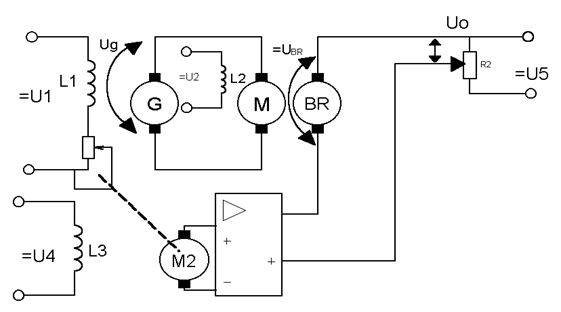
Рассматриваемый принцип основан на том, что управляющее воздействие в САУ выбираются в зависимости от результатов измерения возмущающего воздействия, оказывающего влияние на ОУ. Функциональная схема управления такой САУ имеет вид:
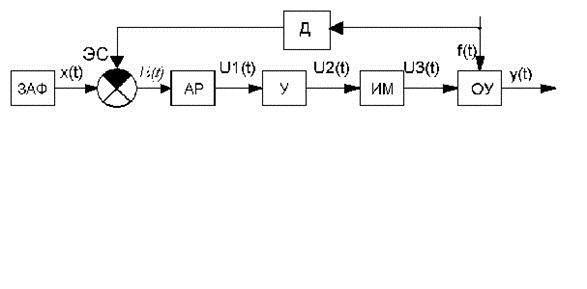
Пример реализации принципа компенсации возмущения (управления по нагрузке):
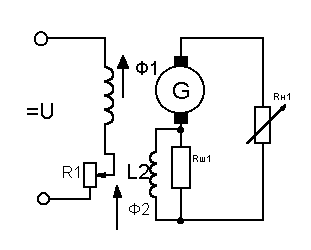
Напряжение на выходе генератора UГ — пропорционально суммарному магнитному потоку. Увеличение или уменьшение тока нагрузки зависит от сопротивления нагрузки. Такое изменение тока нагрузки не окажет никакого влияния на выходное напряжение генератора, т.к. ток нагрузки пропорционален магнитному потоку Ф2 и компенсирует изменение Ф1, т.е. значение суммарного потока постоянно при любых колебаниях нагрузки. Такой принцип носит название принципа управления по нагрузки.
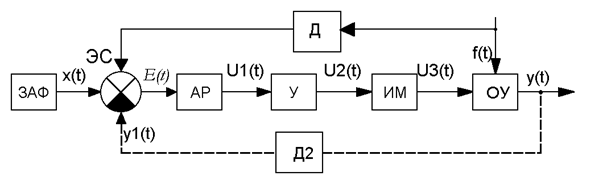
4. Принцип комбинированного управления.
Данный принцип реализуется путем совмещения двух принципов:
1. Принцип управления по отклонению.
2. Принцип управления по возмущению.
Совмещение этих двух принципов дает возможность улучшить качество управления, т.е. предписанное значение регулируемой величины будет более точно с меньшей погрешностью воспроизводиться на выходе системы.
Основные элементы автоматики.
Любая САУ состоит из отдельно связанных между собой элементов.
Элементом автоматики называют часть системы, в которой происходит качественные или количественные преобразования физической величины, а также передача преобразованного воздействия от предыдущего элемента к последующему. Каждый такой элемент выполняет определенные функции, которые для него определяют технологический процесс или функционирование самой системы. Таких элементов в автоматике достаточно много. Рассмотрим основную группу этих элементов.
1. Датчики автоматики — это устройства, которые измеряют управляемые или регулируемые величины объектов управления и преобразовывают измеренные величины одной физической природы в другую (термосопротивления, термопары, переменные конденсаторы, фотоэлемент, тензодатчик и т.д.)
2. Элементы сравнения — они сопоставляют задающее воздействие x(t) и управляемую величину y(t). Получаемая на выходе таких элементов разность e(t)=x(t)-y(t) передается по цепи воздействия, либо непосредственно на исполнительный механизм. Элементы сравнения, как самостоятельная часть системы не применяется, а является составной частью других устройств, например, автоматических регуляторов (эл. мостовые схемы сравнения, потенциометры, пружинные элементы и др.)
3. Усилители — они в системах автоматики обычно используются для усиления задающего воздействия x(t) или разности e(t), когда мощности самих сигналов недостаточно для работы регуляторов (электронные, ионные, магнитные, электромагнитные усилители, редуктор, гидравлические усилители).
4. Исполнительные механизмы — они предназначены для измерения управляемых величин, или поддержания их в заданных пределах. Они предназначены для выработки более мощного воздействия на ОУ, нежели выходной сигнал регулятора (эл. двигатели — серводвигатели; соленоиды; гидро- и пневмодвигатели и т.д.).
5. Задающие элементы (элементы настройки). Они представляют собой устройства, при помощи которых в САУ подается задающее воздействие x(t) (потенциометры, вращающиеся трансформаторы и т.д.).
6. Корректирующие элементы — они предназначаются для улучшения регулировочных свойств системы в целом, или отдельных ее частей (дифференцирующие и интегрирующие цепи, нелинейные элементы и т.д.).
7. Командоаппараты — они предназначены для подачи в систему различных воздействий и команд (кнопки, выключатели, конечные выключатели и т.д.).
8. Элементы защиты — они предназначены для выполнения защитных функций, при недопустимых режимах работы (токовые реле, электротепловые реле, автоматические выключатели, предохранители и т.д.).
9. Контрольно-измерительные приборы — устройства для измерения и контроля различных величин и параметров (показывающие, самопишущие и т.д.).
Также к элементам автоматики относят автоматические регуляторы, объекты управления, сигнальная аппаратура.
Все элементы автоматики обычно указывают на функциональных и структурных схемах, внутри которых указывается либо назначение прибора, либо его передаточная функция и обязательно показывается действующие на элемент входные и выходные воздействия.
Функции и параметры элементов автоматики.
Каждый функциональный элемент выполняет элементарную функцию, которая заключается в получении преобразовании и передачи информации в виде сигналов определенной физической природы. Функциональные элементы предполагают устройствами одно направленного действия, т.е. передающими сигналы в одном направлении.
Всем элементам автоматики, независимо от их назначения присущи общие параметры:
1. Статическая характеристика;
2. Динамическая характеристика;
3. Передаточный коэффициент;
4. Погрешность;
5. Порог чувствительности.
1. Под статической характеристикой элемента понимают зависимость y=f(x), т.е. зависимость между выходными (у) и входными (х) величинами в установившемся режиме, когда х и у неизменны во времени. Статическая характеристика может задаваться в виде аналитического выражения или графика. По виду статической характеристики различают элементы с линейной и нелинейной статической характеристикой.
2. Под динамической характеристикой элемента понимают зависимость выходной величины у от входной величины х в переходном, т.е. динамическом режиме, когда х и у меняются во времени. Характер динамической характеристики зависит от инерционных свойств конкретного элемента. Иногда под динамическими характеристиками понимают зависимость выходной величины у и входной величины х от времени, при переходном процессе.
3. Передаточный коэффициент элемента представляет собой отношение выходной величины у к входной величине х.
Статический коэффициент передачи:
1.7
Динамический коэффициент передачи:
=
=
1.8
Для линейной статической характеристики при всех х и у кс=кД. Единица измерения передаточного коэффициента равна отношению единиц измерения выходной и входной величин. Очень часто на практике используют безразмерный относительный передаточный коэффициент.
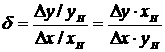1.9
где хн, yн — нелинейные значения х и у.
Коэффициент передачи для разных элементов автоматики называют по разному: для датчиков — коэффициентом чувствительности, для измерителей — коэффициентом усиления и т.д.
4. Погрешностью называется разность между текущим и номинальным заданным значением выходной величины. Различают абсолютную и относительную погрешности, которые возникают из-за изменения внутренних свойств элемента (износ, старение) и внешних условий (изменение температуры и влажности окружающей среды, изменение напряжения питания, изменение частоты тока и т.д.)
5. Порог чувствительности — наименьшее изменение входной величины, способное вызвать появление изменения выходной величины (за счет наличия трения, люфтов, гистерезиса и т.д.).
В отдельных элементах автоматики можно рассматривать различные характеристики, которые отражают работу этих элементов, как части САУ: потребляемая мощность, входное и выходное сопротивление, и т.д.
Очень большому количеству элементов присуще самопроизвольное изменение выходной величины при постоянстве входной. Такие изменения называются: помехами, шумами, дрейфом нуля, плаванием коэффициента усиления.
Математическое описание САУ. Режимы движения автоматических систем.
Математическое описание элементов и систем применяют в тех случаях, когда необходимо изучить систему и элементы в процессе работы, при наличии возмущающих и управляющих воздействий. Математическое описание может быть аналитическим, графическим или табличным. Для получения математического описания системы обычно составляют описание ее отдельных элементов. Совокупность всех уравнений элементов и дает уравнение САУ.
Уравнение, а также структурная схема САУ носит название математической модели системы. Такое название обусловлено тем, что при математическом описании, т.е. составлении уравнений, физических процессов всегда делают какие-либо допущения и приближения. Математическая модель одной и той же системы в зависимости от цели исследования может быть разной. Исследования начинаются с простейших моделей и усложняются в процессе решения.
Если возмущающее и управляющее воздействие в системе непрерывно изменяются, то система находится в динамическом режиме. Динамическим режимом называется такой режим, в котором основным состоянием системы является неустановившееся состояние. Неустановившееся состояние характеризуется тем, что действующее на элемент или систему воздействие вызывает в системе или элементе ряд переходных процессов. При поступлении на вход системы воздействия ее движение складывается из собственного или свободного движения и из реакции на входное воздействие, т.е. из вынужденного движения. Переходной процесс представляет собой такое собственное или свободное движение системы, которое зависит от динамических свойств элементов системы и начальных условий. Собственное движение устойчивой системы с течением времени затухает и она приходит в установившееся состояние. В установившемся состоянии обязательно все воздействия остаются неизменными.
Режим, который характеризуется установившимся процессом в элементе или системе называется статическим.
Действующая САУ, находящаяся в динамическом режиме и ее описание является основным. Статический режим в САУ представляет собою в определенной степени идеализацию, которую принимают для описания элемента или системы после окончания переходного процесса.
Описание элементов и систем в статическом режиме. Линеаризация.
Статический режим это установившееся состояние равновесия, при постоянном воздействии. Он наступает после окончания переходного процесса. Статической характеристикой элемента или системы называется зависимость выходной величины от входной в статическом режиме. В большинстве случаев статическую характеристику изображают в виде графиков, по оси абцисс — х, а по оси ординат — у. Статические характеристики могут иметь следующий вид:
1. линейный
2. нелинейный
3. существенно нелинейный
В реальных случаях статическая характеристика элементов и систем являются нелинейными. В инженерной практике нелинейные характеристики заменяют приближенными линейными. Процесс замены нелинейной характеристики ее линейным приближением называют ее линеаризации.
Наиболее простая линеаризация — это метод осреднения. Он используется в том случае, когда дана достаточно гладкая нелинейная характеристика и ее можно просто заменить линейным выражением или линейным графиком.
Метод малых отклонений. Он основан на замене нелинейной характеристики у=f(x) в окрестности точки А(х0,у0) прямой, касательной к данной точке.
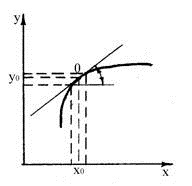
Аналитическая линеаризация нелинейной зависимости в общем случае выполняется с использованием разложения функции у=f(x) в ряд Тейлора для точки равновесного состояния системы. Пусть точка А(х0,у0) является точкой равновесного состояния системы, тогда:
1.10
Затем производится исключения из ряда членов высших порядков малости, т.е. содержащих отклонение величины Dх в степени выше первой:
1.11
1.12
1.13
Выражение (1.13) представляет собой линеаризованную функцию у(х), представленную в отклонениях от равновесного состояния. Производная этой функции в точке равновесного состояния равна тангенсу угла наклона a линеаризованного участка в окрестностях этой точки.
Метод линеаризации применим в случае, если нелинейная функция у=f(x) в окрестности исследуемой точки является непрерывным, а к кривой, изображающую функцию можно провести касательную.
Описание элементов и систем в динамическом режиме. Определение элементарного звена и его дифференциальное уравнение.
Зависимость выходных величин от входных в динамическом режиме записывается в виде дифференциальных или разностных уравнений, в которых независимой переменной является время. Для теоретического исследования САУ необходима оценка каждого ее элемента не по устройству и назначению, а по зависимости от вида описывающего этот элемент. Благодаря тому, что многие элементы отличающиеся между собой по конструкции или по физической природе характеризуются однотипными уравнениями динамики, создается возможность все эти элементы представлять одной типовой моделью. Однако, такие модели могут оказаться достаточно сложными, а их число большим, что затрудняет исследование динамических свойств системы. Поэтому в теории автоматического управления элементы систем с точки зрения их динамических свойств представляют с помощью небольшого числа элементарных динамических звеньев.
Под элементарным динамическим звеном понимается искусственно выделяемая часть автоматической системы, соответствующая какому-либо элементарному алгоритму. Необходимо помнить, что звено обладает направленностью действий, т.е. направлением прохождения сигнала с входа на выход. Уравнение динамики всей системы можно получить из уравнений ее звеньев.
Типовые элементарные звенья характеризуются свойствами линейности и стационарности.
Звено называется линейным, если выходная величина y(t) связана с входной x(t) линейной зависимостью. Звено называется стационарным, если его реакция не зависит от времени.
Элементарные звенья описываются дифференциальными уравнениями не выше второго порядка. Если функциональный элемент или система описывается уравнением высокого порядка, то его математическая модель может быть представлена посредством нескольких элементарных звеньев.
Математическую модель элементарного звена в общем виде можно представить как:
1.14
где а0,а1,а2,b0,b1,b2 — постоянные коэффициенты входной и выходной величины.
Операторная форма записи дифференциального уравнения. Передаточная функция.
Динамика функциональных элементов и систем управления описывается дифференциальным уравнением, которое в общем виде можно записать как
1.15
Необходимо, чтобы n >m, для работы системы. Описание существенно упрощается если от дифференциального уравнения перейти к операторной форме. Для этого необходимо операцию дифференцирования заменить на оператор дифференцирования
р1 — оператор дифференцирования
В результате такой замены мы получили алгебраическое уравнение
1.16
Если в уравнении (1.15) вместо функции времени у(t) и х(t) ввести функции х(р) и у(р) комплексного переменного р=α±jβ , поставив условием что записанные функции связаны отношением
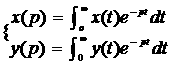1.17
то оказывается что дифференциальное уравнение, содержащие х(t) и у(t) равносильно алгебраическому уравнению вида
1.18
Следует отметить, что трансформация дифференциального уравнения в представленное алгебраическое возможно только при нулевых начальных условиях. И это преобразование в математике называют преобразованием Лапласа. Функции х(р) и у(р) называют изображениями функций х(t) и у(t), а сами функции х(t) и у(t) называют оригиналами функций х(р) и у(р).
Переход от искомой функции у(t) к изображению у(р) называют прямым преобразованием Лапласа, и обозначают
1.19
Переход же от изображения у(р) к оригиналу у(t) называют обратным преобразованием Лапласа
1.20
Из сравнения уравнений (1.18) и (1.16) видно, что обе формы записи совпадают, из чего следует, что оператор дифференцирования отождествляется с комплексной переменной р при нулевых начальных условиях.
Использование операторной формы представления уравнений позволяет избежать решения дифференциальных уравнений путем решения системы алгебраических уравнений. Нахождение оригиналов по изображениям можно провести используя либо справочные таблицы, либо формулу разложения.
Взяв за основу формулу (1.18) можно найти отношение
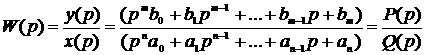1.21
Передаточной функцией W(р) называют отношение изображения по Лапласу выходной величины к изображению входной величины при нулевых начальных условиях.
Из уравнения (1.21) можно записать
1.22
Многочлен, фигурирующий в знаменателе передаточной функции называется характеристическим многочленом, а в случае приравнивания его у нулю уравнение называется характеристическим.
1.23
Корни характеристического уравнения называют полюсами передаточной функции. Корни многочлена, расположенного в числителе передаточной функции, называют нулями передаточной функции.
Понятие о типовых входных сигналах (воздействиях).
Оценку динамических свойств САУ, т.е. их поведение в переходных режимах можно выполнить различными методами. Решение динамического уравнения, которым описывается звено или система при заданных начальных условиях также отображает их динамику. Оно представляет переходный процесс звена или системы во времени. Для сравнения различных динамических свойств различных элементов рассматривают их переходные процессы, при нулевых начальных условиях и типовых входных воздействий.
Начальные условия — это значение выходной величины, а также всех ее производных в момент времени равное нулю, при условии, что до этого времени внешнее воздействие отсутствовали. Эти начальные условия являются нулевыми, т.к. y(t0)=y´(0)=…=yn(0)=0.
В качестве типовых входных воздействий принимают определенные формы воздействий, наиболее удобные с точки зрения их математического описания, практической реализации и описания реакции звена на эти воздействия. Иными словами, входное воздействие должно быть простым, не затрудняющим решение уравнения и соответствовать самому тяжелому режиму работы системы из числа встречающихся при ее эксплуатации.
Различают типовые входные воздействия, описываемые следующими функциями:
1. ступенчатой
2. импульсной
3. гармонической
Первые две функции представляют собой временные характеристики звена или системы, а последняя — частотные характеристики.
1. Единичное ступенчатое воздействие.
Оно описывается единичной ступенчатой функцией:
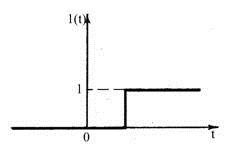
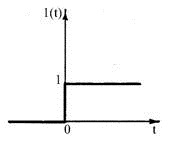а) "Включение" 1(t)
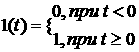1.24
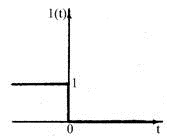б) "Отключение" 1(t)
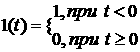1.25
в) "Включение с задержкой"
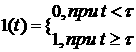1.26
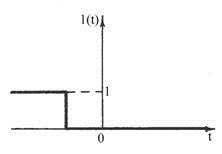г) "Отключение с задержкой"
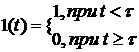1.27
2. Импульсное воздействие (единичный импульс).
Импульсное воздействие описывается единичной импульсной функцией d — Дирака (d(t)) является математической идеализацией короткого импульса, площадь которого равна единице, при его длительности равной нулю и амплитуде равной +¥:
 |
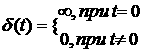1.28
Свойство d(t): площадь этой функции равна 1:
1.29
1.30
3. Гармоническое воздействие.
Такое воздействие описывается гармонической функцией вида:
1.31
Если к звену или системе приложено воздействие, отличающегося от ступенчатого или импульсного, то его представляют в виде суммы последовательных импульсных или ступенчатых воздействий на звено или систему. Реакция звена или системы на такое воздействие может быть получено с использованием интеграла Дюамеля.
Временные характеристики
К временным характеристикам относятся:
1. Переходная функция — реакция звена или системы на единичную ступенчатую функцию при нулевых начальных условиях, называется переходной функцией, которую обозначают как h(t) и при x=1(t) имеем:
1.32
Или переходя от изображения к оригиналу:
1.33
Графическое изображение переходной функции называется переходной характеристикой звена. Покажем наиболее распространенные переходные характеристики:
 |
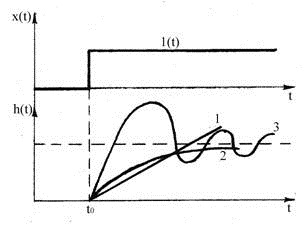1. линейная, установившаяся.
2. апериодическая.
3. колебательная, затухающая.
2. Переходная импульсная функция (функция веса или весовая функция)
Нормальная реакция звена на импульсную функцию называется импульсной переходной функцией или функцией веса, и обозначается w(t). Между импульсной переходной функцией и переходной функцией существует связь:
1.34
1.35
Между передаточной функцией и импульсной переходной функцией существует связь:
1.36
1.37
Графическое изображение весовой функции называют импульсной переходной характеристикой звена или системы.
Частотные характеристики
Кроме описания элементов и систем управления временными характеристиками и передаточными функциями в теории автоматического управления также используют и частотные характеристики. Для получения частотных характеристик на вход элемента или системы подают гармонично изменяющийся сигнал. Если на вход подать сигнал в виде гармонической функции то реакция в установившемся режиме также будет гармонической функции, у которой частота остается равной входной, а амплитуда и фаза в процессе передачи изменятся.
Изменение амплитуды и фазы зависят как от свойств звена в системе, так и от частоты гармонического входного воздействия.
Отношение амплитуды выходного сигнала к амплитуде входного, в зависимости от частоты называется амплитудно-частотной характеристикой (АЧХ) звена или системы:
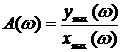1.38
Разность фаз колебаний, в зависимости от частоты называют фазочастотной характеристикой (ФЧХ) звена или системы:
1.39
Частотные характеристики звена или системы зависят только от их свойств, но не зависят от амплитуды и фазы входных гармонических воздействий. Чтобы проследить взаимосвязь между частотными характеристиками или динамическими уравнениями представим входные и выходные воздействия в следующем виде:
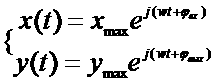1.40
Возьмем производные от рассматриваемых воздействий:
Представим полученное выражение системы (1.40) в уравнение (1.15) и в результате будем иметь выражение вида:
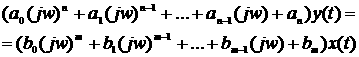1.41
Взяв отношение выходного сигнала ко входному получим выражение, напоминающее передаточную функцию, но записанной через частотные характеристики
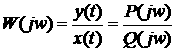1.42
Выражение (1.42) называют частотной характеристикой линейной САУ или что эквивалентно комплексной частотной функции. Функция W(jw) получается из передаточной функции путем подстановки в последнюю вместо оператора Лапласа произведение jw. Функция W(jw), при каждом значении w является комплексной величиной и поэтому может быть представлена в показательной форме как:
1.43
где А(w) — модуль функции W(jw);
j(w) — аргумент частотной функции W(jw).
Функцию W(jw) также принято называть частотной передаточной функцией или частотным передаточным коэффициентом.
Годограф вектора W(jw), при изменении частоты w от 0 до +¥ называют амплитудно-фазовой характеристикой (АФХ или АФЧХ).
Частотные характеристики связаны друг с другом следующими соотношениями:
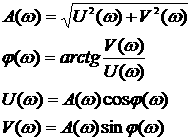1.44
Логарифмические частотные характеристики (ЛАЧХ)
Для инженерных расчетов более удобно использовать не частотные, а логарифмические частотные характеристики. Они представляют собой построение АЧХ и ФЧХ в логарифмическом масштабе. Простота использования таких характеристик определяется тем, что для получения результирующих характеристик можно графически складывать частотные характеристики, а для типовых динамических звеньев можно элементарно просто строить асимптотические ЛАЧХ, т.е. характеристики в виде ломанных линий из прямолинейных отрезков, к которым асимптотически приближаются действительные ЛАЧХ, рассматриваемых динамических звеньев.
По оси абсцисс в таких координатных сетках откладывают частоту в логарифмическом масштабе. За единицу принимается декада (при десятикратной разнице в частотах) или октава (двукратной разнице в частотах). Декада и октава — это акустические единицы.
По оси ординат в равновесном масштабе откладывают логарифмическую амплитуду.
1.45
Единица измерения L(w) принят дБ. Белл — логарифмическая единица, соответствующая десятикратному увеличению мощности. При построении логарифмических характеристик по оси ординат откладывают логарифмическую амплитуду в дБ и аргумент j в градусах или радианах, а по оси абсцисс lg(w) в декадах.
Типовые динамические звенья
Элементы и САУ, описываемые динамическими уравнениями могут быть представлены элементарными звеньями. Число типов элементарных звеньев ограничены и по разным классификационным признакам они объединены в группу:
1. Простые звенья:
1) безынерционное звено (усилительное или пропорциональное звено).
2) интегрирующее звено.
3) дифференцирующее звено.
2. Звенья первого и второго порядка.
1) апериодическое звено первого порядка.
2) колебательное звено.
3) консервативное звено.
4) апериодическое звено второго порядка.
3. Трансцендентные звенья.
1) звено транспортного запаздывания
2) звено чистого запаздывания
Изучение типовых звеньев будем проводить в следующем порядке:
1. Определение и динамическое уравнение звена.
2. Передаточная функция.
3. Примеры звеньев.
4. Переходная функция и функция веса.
5. Переходная и переходная импульсная характеристики.
6. Аналитические выражения АЧХ, ФЧХ, ЛАЧХ и АФЧХ.
7. Изображение ЛЧХ, АФЧХ, ФЧХ, ЛАЧХ.
Безынерционное звено
Это звено относится к группе простейших звеньев, выходная величена в которых пропорциональна входной величине, ее интегралу или производной.
Безынерционным или пропорциональным называется звено, которое как и в переходном, так и в установившемся режиме описывается уравнением:
1.46
где к — коэффициент передачи или пропорциональности.
Предполагается, что реакция звена на входное воздействие происходит мгновенно без всякой инерции. Устройство считается безинерционным, если его инерционность значительно меньше (на несколько порядков) инерционности других устройств, входящих в систему.
Примеры безынерционных звеньев:
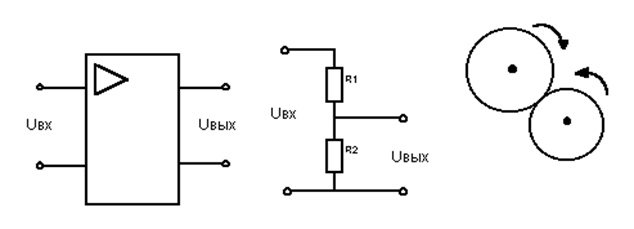
усилитель делитель напряжения редуктор
Передаточная функция этого звена:
1.47
Переходная функция:
 |
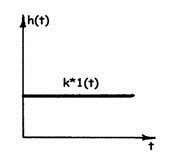1.48
Весовая функция:
 |
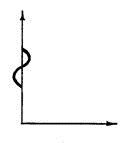1.49
Частотные характеристики:
1.50
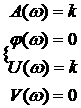1.51
Вид частотных характеристик:
АФХ АЧХ ФЧХ
 |
|||
 |
|||
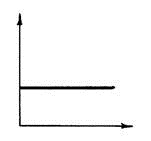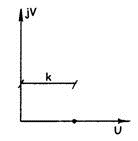φ(ω)=0
Логарифмические частотные характеристики:
1.52
Вид логарифмических характеристик:
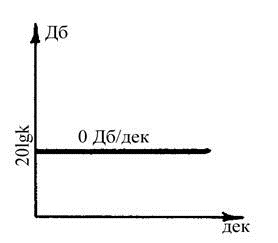
Интегрирующее звено
Интегрирующее звено — это звено у которого выходная величина пропорциональна интегралу по времени от входной величены.
1.53
1.54
где к — коэффициент пропорциональности данного звена.
Скорость изменения выходной величены интегрирующего звена, пропорциональна входной величине.
Примеры:
а) Резервуар с водой
б) Двигатель постоянного тока.
в) Напряжение на конденсаторе.
Уравнение (1.54) можно переписать в операторной форме:
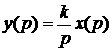1.55
Передаточная функция этого звена:
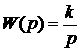1.56
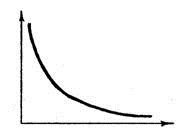
Переходная функция:
 |
1.57
Весовая функция:
 |
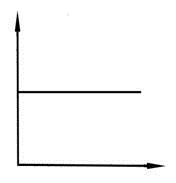1.58
Частотные характеристики:
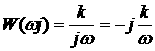1.59
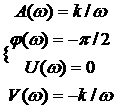1.60
Вид частотных характеристик:
АФХ АЧХ ФЧХ
 |
|||||
 |
|||||
 |
|||||
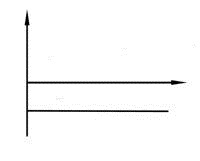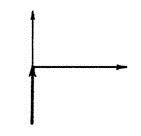Логарифмические частотные характеристики:
1.61
Вид логарифмических характеристик:
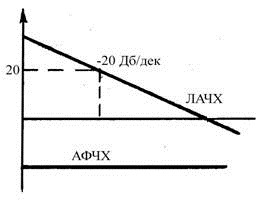
Дифференцирующее звено.
Дифференцирующем называют звено, у которого в установившемся режиме выходная величина пропорциональна дифференциалу входной величены.
1.62
Или в операторной форме:
1.63
В реальных условиях не существует такого реального элемента, который бы на выходе точно воспроизводил бы производную от входного сигнала. Идеализированными примерами такого звена могут быть:
а) Тахогенератор.
б) Ток через электроконденсатор.
Передаточная функция этого звена:
1.64
Переходная функция:
![clip_image142[1]](/images/stories/clip_image142-1_thumb.jpg "clip_image142[1]") |
1.65
Весовая функция:
1.66
Частотные характеристики:
1.67
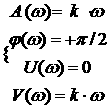1.68
Вид частотных характеристик:
АФХ АЧХ ФЧХ
 |
|||||
 |
|||||
 |
|||||
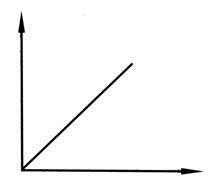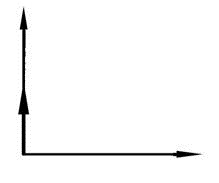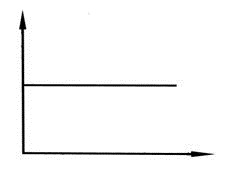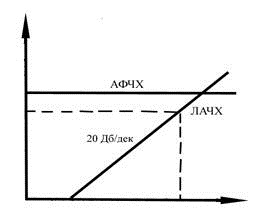
Логарифмические частотные характеристики:
1.69
Вид логарифмических характеристик:
Апериодическое (инерционное) звено первого порядка
Апериодическим называется такое звено, у которого выходная величина после подачи на вход ступенчатого воздействия изменяется монотонно, достигая некоторого установившегося значения.
1.70
Дифференциальное уравнение в операторной форме
1.71
Апериодические звенья первого порядка наиболее часто применяются в практике автоматического регулирования.
Примеры звеньев:
1)нагрев тела
2)RC-цепь
 |
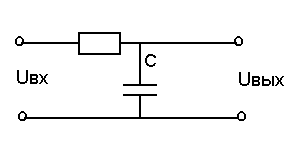Передаточная функция
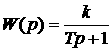1.72
Переходная функция
 |
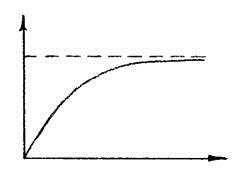1.73
Функция веса
 |
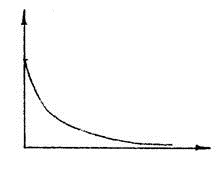1.74
Для рассматриваемого звена временной характеристикой может служить решение дифференциального уравнения (1.70).
1.75
Из выражения (1.75) можно перейти к выражению (1.73), если на вход подать ступенчатое воздействие, а начальные координаты принять равные нулю.
Теоретически, переходный процесс у звеньев рассматриваемого типа, длится бесконечно долго. Практически же, для апериодического звена, переходный процесс может быть завершенным, если выходная величина достигает значения 0,95-0,99 от установившегося. Такой промежуток времени определяется значениями (3Т...5Т).
Частотные характеристики
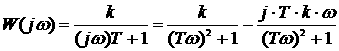1.76
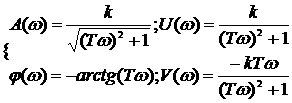1.77
Вид частотных характеристик
АФХ АЧХ ФЧХ
 |
|||||
 |
|||||
 |
|||||
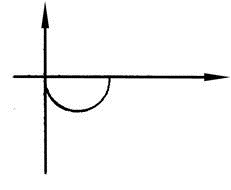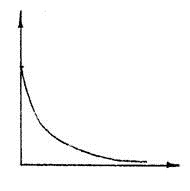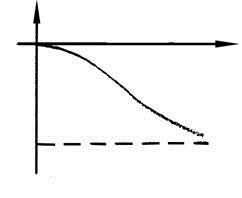Выражение для ЛАЧХ
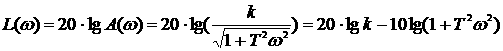1.78
Выражение для аналитической ЛАЧХ
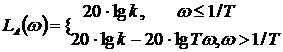1.79
Вид логарифмических характеристик
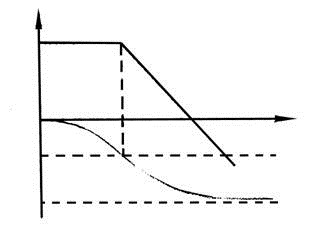
Колебательное звено
Колебательное звено в динамическом режиме описывается операторным уравнением
где Т1 и Т2 — постоянные времени, характеризующие период и время затухания собственных колебаний звена (при Т1 <2Т2);
к — коэффициент усиления звена.
Колебательное звено отличается тем, что при изменении входной величины x возникает колебательный процесс изменения выходной величины y. Уравнение передаточной функции и АФЧХ колебательного звена выражается аналогично как и для апериодического звена второго порядка.
Временная характеристика
 |
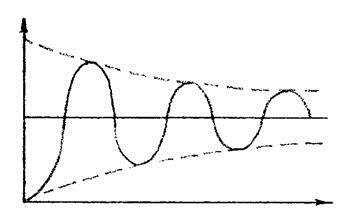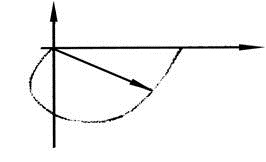
АФЧХ при входном воздействии типа единичного скачка
 |
Колебательное звено можно рассматривать как соединение двух емкостей, способных записать энергию или вещество и взаимно обмениваться этими запасами при возмущениях, нарушающих равновесие звена возникшего колебания. Если в результате колебания происходит потеря энергии в звене, то колебания затухают, а само звено называется устойчивым.
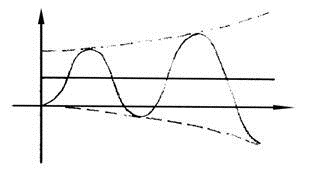
Выше речь шла об устойчивом колебательном звене. Если же при колебаниях запас энергии в звене увеличивается, то амплитуда колебания возрастает, а само звено называется неустойчивым. Уравнение динамики неустойчивого колебательного звена в операторной форме
Временная характеристика
 |
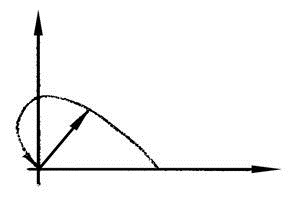
АФЧХ
 |
Консервативное звено
Если при колебании отсутствует потери энергии в звене, то такое звено называется колебательным консервативным.
Уравнение динамики консервативного звена в операторной форме при Т1=0.
Передаточная функция
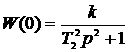
АФЧХ и временная характеристика
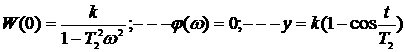
Временная характеристика
 |
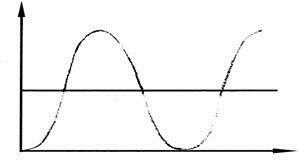АФЧХ
 |
АФЧХ при изменении ω от 0 до бесконечности начинается на положительной вещественной оси на расстоянии к от начала координат и уходит в бесконечность, а возвращается от минус бесконечности по оси отрицательных вещественных чисел.
Апериодическое звено второго порядка
Апериодическое звено второго порядка выражается следующим уравнением в операторной форме
Физический смысл последнего неравенства заключается в том, что потери энергии в звене очень велики и колебания в нем не возникают. Апериодическое звено может быть представлено, как два последовательно включенных звена первого порядка.
Временная характеристика апериодического звена второго порядка
 |
АФЧХ
 |
Уравнение передаточной функции и АФЧХ апериодического звена второго порядка записываются выражениями
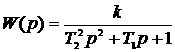
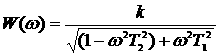
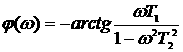
К апериодическому звену второго порядка относятся нагревательные установки, отопительные печи, сушильные агрегаты, теплицы, животноводческие помещения и т. п.
Звено транспортного запаздывания
Это звено относится к транспортным звеньям, т. е. звеньям, которые описываются не алгебраическими передаточными функциями. Звено транспортного запаздывания описывается уравнением вида:
1.80
Звено запаздывания осуществляет операцию сдвига входного сигнала на время τ назад. Выходная величина равна входной, но сдвинута на время τ.
Примеры звеньев:
 |
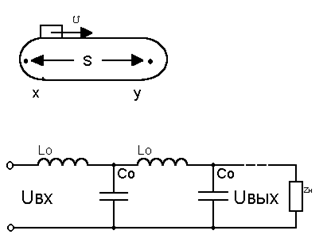транспортер
длинная линия электрической передачи без потерь с распределенными параметрами
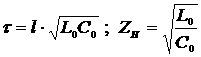
Примерами звеньев с запаздыванием могут служить трубопроводы, водопроводы и другие протяжные конструкции.
Для того чтобы получить передаточную функцию необходимо x(t-τ) разложить в ряд Тейлора:
1.81
Перепишем выражение (1.81) в операторную форму, в результате чего получим выражение
1.82
Экспоненциальная зависимость
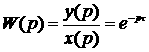1.83
Переходная функция
1.84
Весовая функция
1.85
Временные характеристики
Частотные характеристики
1.86
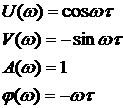1.87
Вид частотных характеристик
АФХ АЧХ ФЧХ
 |
Логарифмические частотные характеристики
Объекты управления и их свойства.
Объекты управления являются теми основными элементами системы управления и регулирования, в которых при помощи технических средств автоматики должен осуществляться заданный или предписанный алгоритм функционирования. Объектом управления может быть машина, набор машин или сооружение, которые предназначены для выполнения технологического процесса, целью которого является получение определенной продукции или энергии. В состав объекта управления может также входить внешняя среда, если она оказывает существенное влияние на состояние объекта. Особенность объекта управления заключается в том, что в нем происходит преобразование, передача или накопление энергии или вещества.
Подведенная из вне энергия или вещество изменяют состояние объекта, которое прежде всего характеризуется изменением его параметров.
Для изменения подводимой энергии или вещества к объекту, последний обязательно имеет регулирующий орган.
Объект можно считать управляемым, если он характеризуется следующими признаками:
а) в нем происходит преобразование, передача или накопление энергии или вещества;
б) если он имеет регулирующий орган для изменения потока энергии или вещества;
в) приток энергии или вещества изменяет состояние объекта, которое характеризуется изменением одного или нескольких параметров, определяющих алгоритм функционирования и составляющих цепь управления.
Воздействие на объект управления может осуществляться как на стороне поступления энергии или вещества, так и на выходе их из объекта. Обычно воздействие на объект управления определяют как управляющим или как возмущающим.
Параметры объекта управления обычно характеризуют качество управления и их называют переменными управления или выходными величинами управляющего объекта.
Объект управления характеризуется определенными свойствами, которые влияют на работоспособность объекта и качества протекающих в цепи процессов.
К основным свойствам объекта управления относят самовыравнивание, запаздывание и аккумулирующую способность.
Под самовыравниванием понимают способность объекта самостоятельно приходить в новое состояние равновесия при изменении управляющего или возмущающего воздействия. Свойством самовыравнивания обладают не все объекты управления. Объекты управления которые описываются интегральными или интегрирующими звеньями не обладают самовыравниванием. Такие объекты называются астатическими, а обладающие самовыравниванием — статические.
Объекты без самовыравнивания очень трудно поддаются управлению. Самовыравнивание может быть положительным и отрицательным. В первом случае равновесие восстанавливается без участия регулятора. В случае отрицательного самовыравнивания, восстановление равновесия осуществляется только при участии регулятора. Это объясняется тем, что возникшее нарушение в объекте стремится к накоплению. При отрицательном самовыравнивании объект называется неустойчивым статическим, а при положительном — устойчивым статическим объектом.
Количественно самовыравнивание описывается коэффициентом самовыравнивания, который равен отношению производной от приращения внешнего воздействия к производной от управляемой величины
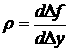1.89
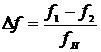– приращение возмущения;
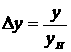– приращение управляемой величины.
Чем больше коэффициент ρ, тем легче осуществляется процесс автоматического управления, т.к. меньше отклонение управляемой величины, а следовательно процесс управления протекает быстрее и качественнее.
Объект с отрицательным самовыравниванием и объект без самовыравнивания не могут работать без регуляторов.
Большинство объектов управления в той или иной мере присуща инерционность, которая вызывает запаздывание во времени между изменением управляющего воздействия и соответствующим изменением управляемой величины. Такое запаздывание в объектах управления может быть переходным и транспортным.
Переходное запаздывание появляется из-за сопротивления перехода вещества из одной емкости в другую или энергии из одного состояния в другое, и всегда наблюдается в тех объектах, где имеются емкости, индуктивности, вращающиеся массы и т. д. Оно определяется как промежуток времени от момента возмущения до начала изменения управляемой величины в результате преодоления имеющихся сопротивлений. Переходное сопротивление отрицательно влияет на процесс управления.
Транспортное запаздывание присуще тем объектам, у которых между управляющим органом и выходом объекта имеются транспортные каналы (трубопроводы, ЛЭП и т. д.). Для прохождения такого канала требуется время, равное отношению длинны канала к скорости движения вещества или энергии.
Разным объектам управления присущи различные запаздывания:
1) одноемкостным объектам присуще только переходное запаздывание
2) двухемкостным и многоемкостным объектам присуще транспортное и переходное запаздывание
3) безъемкостным объектам, запаздывание вообще не присуще
Полное запаздывание объекта определяется суммой всех видов запаздываний в нем.
Опасно влияние любого вида запаздывания на процесс управления в объекте без самовыравнивания.
Любой технологический процесс в том или ином объекте управления связан с притоком, расходом, накоплением и преобразованием некоторой материальной среды или энергии. Многие объекты в процессе работы могут запасать внутри себя рабочую среду, что характеризует аккумулирующую способность рассматриваемого объекта. Аккумулирующая способность достаточно серьезно влияет на регулировочные свойства объекта. Саму эту способность оценивают по емкости объекта, под которым понимают запасенные объектом материал, вещество или энергию. Чем меньше емкость объекта, тем он более чувствителен к возмущающим воздействиям.
Количественно оценить емкость объекта можно при помощи коэффициента емкости, под которым понимают то количество энергии или вещества, которое необходимо подвести к объекту управления или отнести от него чтобы принять управляемую величину на единицу измерения
1.90
y — управляемая величина;
С — емкость объекта.
Значение емкости характеризует запас управляемой величины или среды внутри объекта.
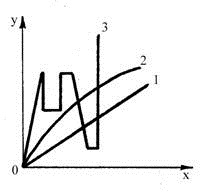
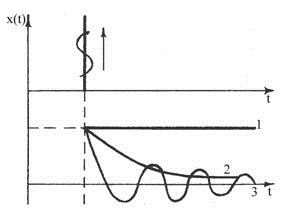
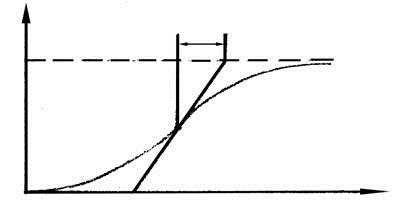
Изменение управляемого параметра во времени, представленное графически, называют кривой разгона. Кривые разгона объектов с различными свойствами
 |
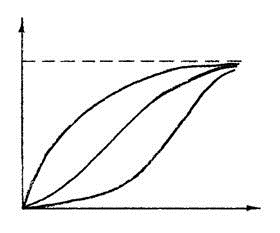1)одноемкостной без передаточного запаздывания
2)многоемкостной без передаточного запаздывания
3) многоемкостной с передаточным запаздыванием
Основные характеристики кривой разгона
 |
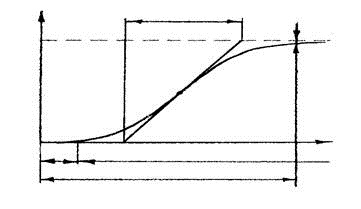T — постоянная времени объекта
Тр — время разгона
τп — транспортное (передаточное) запаздывание
τ0 – переходное запаздывание
yп – точка перегиба
yк – конечное (установившееся) значение управляемой величины
Время разгона — это время от момента подачи возмущения до момента, когда управляемый параметр достигнет нового установившегося значения (в практических целях до 99% установившегося значения).
Постоянная времени — это время разгона объекта без самовыравнивания. Если в объекте есть самовыравнивание и емкость, то постоянная времени равна времени в течение которого отклонение управляемого параметра (yк -y0) от установившегося значения уменьшается в е=2,71 раз.
В практических целях постоянную времени определяют как промежуток времени от момента подачи возмущения до момента, когда управляющий параметр станет равным 0,63 установившегося значения.
Для определения всех вышеназванных временных значений, используют графический метод или формулы
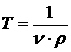1.91
ν – чувствительность объекта к возмущению.
1.92
1.93
