Лекции для студентов

Лекция по автоматике

Частотные характеристики

Кроме описания элементов и систем управления временными характеристиками и передаточными функциями в теории автоматического управления также используют и частотные характеристики. Для получения частотных характеристик на вход элемента или системы подают гармонично изменяющийся сигнал. Если на вход подать сигнал в виде гармонической функции то реакция в установившемся режиме также будет гармонической функции, у которой частота остается равной входной, а амплитуда и фаза в процессе передачи изменятся.

Изменение амплитуды и фазы зависят как от свойств звена в системе, так и от частоты гармонического входного воздействия.

Отношение амплитуды выходного сигнала к амплитуде входного, в зависимости от частоты называется амплитудно-частотной  характеристикой (АЧХ) звена или системы:

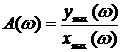                                                     1.38

Разность фаз колебаний, в зависимости от частоты называют фазочастотной характеристикой (ФЧХ) звена или системы:

                                                       1.39

Частотные характеристики звена или системы зависят только от их свойств, но не зависят от амплитуды и фазы входных гармонических воздействий. Чтобы проследить взаимосвязь между частотными характеристиками или динамическими уравнениями представим входные и выходные воздействия в следующем виде:

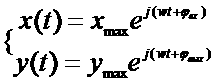                                                1.40

Возьмем производные от рассматриваемых воздействий:

 

Представим полученное выражение системы (1.40) в уравнение (1.15) и в результате будем иметь выражение вида:

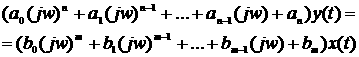                              1.41

Взяв отношение выходного сигнала ко входному получим выражение, напоминающее передаточную функцию, но записанной через частотные характеристики

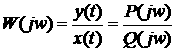                                                     1.42

Выражение (1.42) называют частотной характеристикой линейной САУ или что эквивалентно комплексной частотной функции. Функция W(jw) получается из передаточной функции путем подстановки в последнюю вместо оператора Лапласа произведение jw. Функция W(jw), при каждом значении w является комплексной величиной и поэтому может быть представлена в показательной форме как:

                                       1.43

где А(w) — модуль функции W(jw);

j(w) — аргумент частотной функции W(jw).

Функцию W(jw) также принято называть частотной передаточной функцией или частотным передаточным коэффициентом.

Годограф вектора W(jw), при изменении частоты w от 0 до +¥ называют амплитудно-фазовой характеристикой (АФХ или АФЧХ).

Частотные характеристики связаны друг с другом следующими соотношениями:

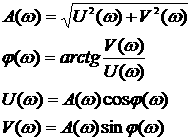                                        1.44