Лекция по автоматике
Описание элементов и систем в статическом режиме. Линеаризация.
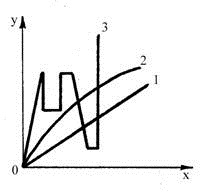
Статический режим это установившееся состояние равновесия, при постоянном воздействии. Он наступает после окончания переходного процесса. Статической характеристикой элемента или системы называется зависимость выходной величины от входной в статическом режиме. В большинстве случаев статическую характеристику изображают в виде графиков, по оси абцисс — х, а по оси ординат — у. Статические характеристики могут иметь следующий вид:
1. линейный
2. нелинейный
3. существенно нелинейный
В реальных случаях статическая характеристика элементов и систем являются нелинейными. В инженерной практике нелинейные характеристики заменяют приближенными линейными. Процесс замены нелинейной характеристики ее линейным приближением называют ее линеаризации.
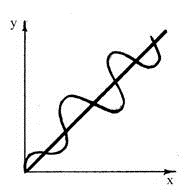
Наиболее простая линеаризация — это метод осреднения. Он используется в том случае, когда дана достаточно гладкая нелинейная характеристика и ее можно просто заменить линейным выражением или линейным графиком.
Метод малых отклонений. Он основан на замене нелинейной характеристики у=f(x) в окрестности точки А(х0,у0) прямой, касательной к данной точке.
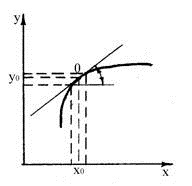
Аналитическая линеаризация нелинейной зависимости в общем случае выполняется с использованием разложения функции у=f(x) в ряд Тейлора для точки равновесного состояния системы. Пусть точка А(х0,у0) является точкой равновесного состояния системы, тогда:
1.10
Затем производится исключения из ряда членов высших порядков малости, т.е. содержащих отклонение величины Dх в степени выше первой:
1.11
1.12
1.13
Выражение (1.13) представляет собой линеаризованную функцию у(х), представленную в отклонениях от равновесного состояния. Производная этой функции в точке равновесного состояния равна тангенсу угла наклона a линеаризованного участка в окрестностях этой точки.
Метод линеаризации применим в случае, если нелинейная функция у=f(x) в окрестности исследуемой точки является непрерывным, а к кривой, изображающую функцию можно провести касательную.
