Лекции для студентов

Электричество и магнетизм. Часть 2

Страница 26 из 28
clip_image049[19]

Лекция 10

Основные уравнения магнитостатики в вакууме.

3.10. Поток вектора магнитной индукции. Теорема Гаусса в магнитостатике. Вихревой характер магнитного поля.

Потоком вектора clip_image879[11]через какую-либо поверхность S называется интеграл:

clip_image1080,

где clip_image1082- проекция вектораclip_image879[12] на нормаль к поверхности S в данной точке (рис.10.1).

clip_image1084

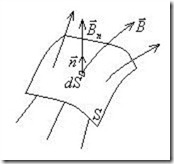
Рис.10.1. К определению потока вектора магнитной индукции.

Прежде чем сформулировать теорему Гаусса в магнитостатике, вспомним, что в электростатике аналогичная теорема формулировалась как:

clip_image1086,

где интеграл берется по замкнутой поверхности S, окружающей электрические заряды (qs – алгебраическая сумма зарядов, заключенных под этой поверхностью); clip_image359[2]- вектор электрической индукции ( в вакуумеclip_image1089).

Казалось бы, что в полной аналогии с электростатикой мы могли бы написать:

clip_image1091,

подразумевая под clip_image1093 алгебраическую сумму неких «магнитных зарядов», охваченных замкнутой поверхностью S, и являющихся источниками магнитных полей с результирующей индукцией clip_image1095 (в вакууме).

Но, как оказалось, в природе нет магнитных зарядов, подобных электрическим, а источниками магнитных полей являются движущиеся заряды, то есть электрические токи. Следует, однако, заметить, что законы классической электродинамики допускают существование частиц с одним магнитным полюсом — магнитных монополей. В квантовой механике магнитный монополь — это стабильная частица, несущая положительный или отрицательный магнитный заряд, величина которого значительно превосходит величину элементарного электрического заряда. Впервые гипотезу о существовании магнитного монополя высказал в 1931г. один из основателей квантовой механики Поль Дирак (Dirac P., 1902-1984), поэтому эту частицу называют также монополем Дирака. Тщательные поиски монополя Дирака не увенчались успехом, поэтому вопрос о их существовании остается пока открытым.

Полагая, таким образом, чтоclip_image1097, приходим к следующей формулировке теоремы Гаусса в магнитостатике:

clip_image1099.

Равенство нулю потока магнитной индукции через произвольную замкнутую поверхность означает, что силовые линии магнитного поля нигде не обрываются и, следовательно, являются замкнутыми (рис.10.2).

clip_image1101

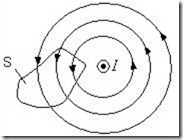
Рис.10.2. К формулировке теоремы Гаусса в магнитостатике.

Поля, силовые линии которых замкнуты, называются вихревыми или соленоидальными.

Вы здесь: Главная Физика Электричество и магнетизм Электричество и магнетизм. Часть 2