Электричество и магнетизм. Часть 2
- Электричество и магнетизм. Часть 2
- 2.2. Закон Ома для однородного участка цепи. Сопротивление проводников.
- 2.3. Дифференциальная форма закона Ома.
- 2.4. Сторонние силы. ЭДС источника тока. Закон Ома для неоднородного участка цепи и для замкнутой цепи.
- 2.5. Напряжение на зажимах источника тока.
- 2.6. Разветвленные цепи. Правила Кирхгофа.
- . 2.7. Соединение сопротивлений.
- 2.8. Работа и мощность постоянного тока. Закон Джоуля — Ленца.
- 2.9. КПД источника тока.
- 2.10. Природа носителей тока в металлах.
- 2.11. Основные положения классической электронной теории проводимости металлов Друде — Лоренца.
- 2.12. Вывод законов Ома, Джоуля-Ленца и Видемана-Франца на основе теории Друде-Лоренца.
- 2.13. Затруднения классической теории электропроводности металлов. Сверхпроводимость металлов.
- 2.14. Электрический ток в электролитах. Законы электролиза Фарадея.
- 2.15. Электропроводность газов. Основные виды газового разряда. Плазма.
- 2.16. Электрический ток в вакууме. Работа выхода электрона из металла.
- 3.1. Взаимодействие проводников с током. Закон Ампера.
- 3.2. Закон Био-Савара-Лапласа. Принцип суперпозиции магнитных полей.
- 3.3. Примеры вычисления магнитных полей с помощью закона Био-Савара-Лапласа.
- 3.4. Магнитный момент тока.
- 3.5. Магнитное поле на оси кругового витка с током.
- 3.6. Момент сил, действующих на контур с током в магнитном поле.
- 3.7. Энергия контура с током в магнитном поле.
- 3.8. Контур с током в неоднородном магнитном поле.
- 3.9. Работа, совершаемая при перемещении контура с током в магнитном поле.
- 3.10. Поток вектора магнитной индукции. Теорема Гаусса в магнитостатике
- 3.11. Теорема о циркуляции магнитного поля. Магнитное напряжение.
- 3.12. Магнитное поле соленоида и тороида.
2.12. Вывод законов Ома, Джоуля-Ленца и Видемана-Франца на основе теории Друде-Лоренца.
Закон Ома.
Ускорение, приобретаемое электроном в электрическом поле 
(рис.6.3).
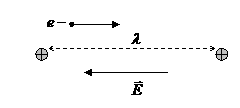
Рис.6.3. К выводу закона Ома.
На пути свободного пробега λ максимальная скорость электрона достигнет величины
,
где τ — время свободного пробега: 
.
Среднее значение скорости упорядоченного движения есть:
.
Подставив это значение в формулу для плотности тока, будем иметь:
,
Полученная формула представляет собой закон Ома в дифференциальной форме:
,
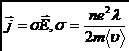где σ — удельная электропроводность металла:
.
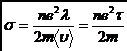Закон Джоуля — Ленца
Кинетическая энергия электрона, которую он имеет к моменту соударения с ионом:
.
При столкновении с ионом энергия, полученная электроном в электрическом поле 
, полностью передается иону. Число соударений одного электрона в единицу времени равно 
, где λ — длина свободного пробега электрона. Общее число столкновений за единицу времени в единице объема равно 
. Тогда количество тепла, выделяющегося в единице объема проводника за единицу времени будет:
.
Последнюю формулу можно представить в виде закона Джоуля-Ленца в дифференциальной форме:
,
где ρ =1/σ — удельное сопротивление металла.
Закон Видемана-Франца.
Из опыта известно, что металлы, наряду с высокой электропроводностью, обладают также высокой теплопроводностью. Видеман (Wiedemann G., 1826-1899) и Франц (Franz R.,) установили в 1853г. эмпирический закон, согласно которому отношение коэффициента теплопроводности κ к коэффициенту электропроводности σ для всех металлов приблизительно одинаково и изменяется пропорционально абсолютной температуре:
.
Рассматривая электроны как одноатомный газ, можем на основании кинетической теории газов написать для коэффициента теплопроводности электронного газа:
,
где 
— удельная теплоемкость одноатомного газа при постоянном объеме.
Разделив κ на σ, приходим к закону Видемана-Франца:
.
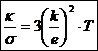Подставив сюда k = 1,38·10-23 Дж/К и е = 1,6·10-19 Кл, найдем, что
,
что очень хорошо согласуется с экспериментальными данными.
