Лекции для студентов

Электричество и магнетизм. Часть 2

2.3. Дифференциальная форма закона Ома.

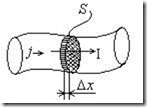
Если проводник неоднороден по своему составу и/или имеет неодинаковое сечение, то для характеристики тока в различных частях проводника используют закон Ома в дифференциальной форме. Для его вывода выделим внутри проводника элементарный цилиндрический объем (рис.5.8) с образующими, параллельными вектору плотности тока . Если выделенный объем достаточно мал, его можно считать однородным и применить к нему закон Ома:

, где

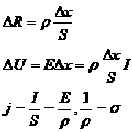, откуда

Рис.5.8. К выводу закона Ома в дифференциальной форме.

Или в векторном виде:

Величина называется коэффициентом электропроводности или проводимостью материала. Единицей измерения σ в СИ является (Ом∙м)^-1=См (сименс).