Лекции для студентов

Электричество и магнетизм. Часть 2

Лекция 5

2. Постоянный электрический ток

2.1. Характеристики тока. Сила и плотность тока. Падение потенциала вдоль проводника с током.

Всякое упорядоченное движение зарядов называется электрическим током. Носителями заряда в проводящих средах могут быть электроны, ионы, «дырки» и даже макроскопические заряженные частицы.

За положительное направление тока принято считать направление движения положительных зарядов. Электрический ток характеризуется силой тока — величиной, определяемой количеством заряда, переносимого через воображаемую площадку, за единицу времени:

Для постоянного тока силу тока можно определить как:

Размерность силы тока в СИ: (ампер).

Кроме этого, для характеристики тока в проводнике применяют понятие плотности тока — векторной величины, определяемой количеством заряда, переносимого за единицу времени через единичную площадку, перпендикулярную линиям тока (рис.5.1):

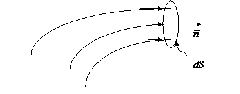Рис.5.1. К определению вектора плотности тока

Размерность плотности тока в СИ: .

Покажем, что плотность тока пропорциональна скорости упорядоченного движения зарядов в проводнике . Действительно, количество заряда, протекающее через поперечное сечение проводника за единицу времени есть (рис.5.2):

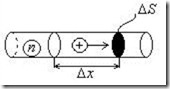, где  — концентрация зарядов

.

Рис.5.2. К выводу формулы для плотности тока.

Или в векторном виде:

Как мы знаем, при равновесии зарядов, то есть при отсутствии тока, потенциал всех точек проводника имеет одно и то же значение, а напряженность электрического поля внутри него равна нулю (рис.5.3а). При наличии тока электрическое поле внутри проводника отлично от нуля, и вдоль проводника с током имеет место падение потенциала (рис.5.3б).

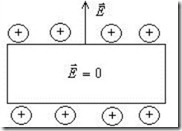Тока нет:

Рис.5.3а. Электрическое поле проводника при отсутствии тока.

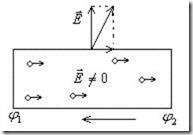Ток есть: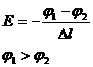

Рис.5.3б. Электрическое поле проводника при наличии тока.

Таким образом, для существования тока в проводнике необходимо выполнение двух условий: 1) наличие носителей заряда и 2) наличие электрического поля в проводнике.