Лекции для студентов

Электричество и магнетизм. Часть 2

Лекция 8

3. МАГНИТОСТАТИКА

Магнитостатика — раздел электродинамики, изучающий взаимодействие постоянныхэлектрических токов и магнитные поля, создаваемые этими токами.

Постоянное магнитное поле.

3.1. Взаимодействие проводников с током. Закон Ампера.

Известно, что постоянный магнит оказывает действие на проводник с током (например, рамку с током); известно также обратное явление — проводник с током оказывает действие на постоянный магнит (например, на магнитную стрелку компаса) — рис.8.1.

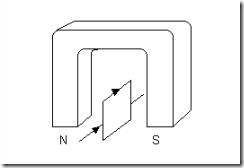
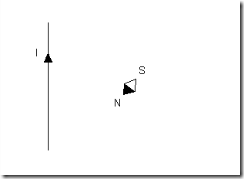
Рис.8.1. Действие постоянного магнита на рамку с током и проводника с током на магнитную стрелку компаса.

Естественно поставить вопрос: а не может ли один проводник с током оказывать непосредственное действие на другой проводник с током? Положительный ответ на этот вопрос дал в 1820г. Ампер (Ampere A., 1775-1836), установивший силовой закон взаимодействия проводников с током.

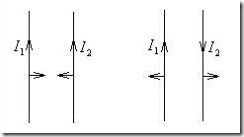
Рис.8.2. Взаимодействие двух прямолинейных проводников с током.

Так, два прямолинейных параллельных проводника (рис.8.2) притягиваются, если токи в них текут в одном направлении и отталкиваются, если токи имеют противоположное направление.

Для того, чтобы сформулировать закон Ампера в современном виде, введем понятие элемента тока как вектора, равного произведению силы тока I на элемент длины проводника (рис.8.3). Элемент тока в магнитостатике играет ту же роль, что и точечный заряд в электростатике.

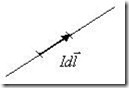
Рис.8.3. Элемент тока.

Своими опытами Ампер установил, что сила взаимодействия двух элементов тока:

1) ;

2) ;

3)  — зависит от взаимной ориентации элементов тока.

Объединяя эти результаты, можем написать закон Ампера в виде:

Углы θ₁ и θ₂ характеризуют ориентацию элементов тока (рис.8.4); Коэффициент пропорциональности k зависит от выбора системы единиц измерения.

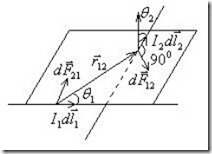
Рис.8.4. Взаимодействие двух элементов тока.

В системе СИ: , где  — магнитная постоянная.

Закон Ампера является аналогом закона Кулона в магнитостатике и выражает собой силу взаимодействия двух элементов тока. Однако в отличие от закона Кулона, он имеет более сложное написание, что обусловлено тем, что элемент тока (в отличие от точечного заряда) характеризуется не только величиной, но и направлением в пространстве. Заметим, что согласно закону Ампера (см. рис.8.4). Это кажущееся противоречие с третьим законом Ньютона связано с тем, что в действительности мы имеем дело не с элементами токов, а с замкнутыми макроскопическими токами, для которых третий закон Ньютона выполняется.

В векторной форме закон Ампера записывается следующим образом:

.