Электричество и магнетизм. Часть 2
- Электричество и магнетизм. Часть 2
- 2.2. Закон Ома для однородного участка цепи. Сопротивление проводников.
- 2.3. Дифференциальная форма закона Ома.
- 2.4. Сторонние силы. ЭДС источника тока. Закон Ома для неоднородного участка цепи и для замкнутой цепи.
- 2.5. Напряжение на зажимах источника тока.
- 2.6. Разветвленные цепи. Правила Кирхгофа.
- . 2.7. Соединение сопротивлений.
- 2.8. Работа и мощность постоянного тока. Закон Джоуля — Ленца.
- 2.9. КПД источника тока.
- 2.10. Природа носителей тока в металлах.
- 2.11. Основные положения классической электронной теории проводимости металлов Друде — Лоренца.
- 2.12. Вывод законов Ома, Джоуля-Ленца и Видемана-Франца на основе теории Друде-Лоренца.
- 2.13. Затруднения классической теории электропроводности металлов. Сверхпроводимость металлов.
- 2.14. Электрический ток в электролитах. Законы электролиза Фарадея.
- 2.15. Электропроводность газов. Основные виды газового разряда. Плазма.
- 2.16. Электрический ток в вакууме. Работа выхода электрона из металла.
- 3.1. Взаимодействие проводников с током. Закон Ампера.
- 3.2. Закон Био-Савара-Лапласа. Принцип суперпозиции магнитных полей.
- 3.3. Примеры вычисления магнитных полей с помощью закона Био-Савара-Лапласа.
- 3.4. Магнитный момент тока.
- 3.5. Магнитное поле на оси кругового витка с током.
- 3.6. Момент сил, действующих на контур с током в магнитном поле.
- 3.7. Энергия контура с током в магнитном поле.
- 3.8. Контур с током в неоднородном магнитном поле.
- 3.9. Работа, совершаемая при перемещении контура с током в магнитном поле.
- 3.10. Поток вектора магнитной индукции. Теорема Гаусса в магнитостатике
- 3.11. Теорема о циркуляции магнитного поля. Магнитное напряжение.
- 3.12. Магнитное поле соленоида и тороида.
3.9. Работа, совершаемая при перемещении контура с током в магнитном поле.
Рассмотрим отрезок проводника с током, способный свободно перемещаться по двум направляющим во внешнем магнитном поле (рис.9.5). Магнитное поле будем считать однородным и направленным под углом α по отношению к нормали к плоскости переме-щения проводника.
|
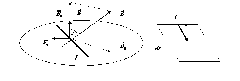
Рис.9.5. Отрезок проводника с током в однородном магнитном поле.
Как видно из рис.9.5, вектор ![]() имеет две составляющие
имеет две составляющие ![]() и
и ![]() , из которых только составляющая
, из которых только составляющая ![]() создает силу, действующую в плоскости перемещения проводника. По абсолютной величине эта сила равна:
создает силу, действующую в плоскости перемещения проводника. По абсолютной величине эта сила равна:
![]() ,
,
где I – сила тока в проводнике; l — длина проводника; B — индукция магнитного поля.
Работа этой силы на элементарном пути перемещения ds есть:
![]() .
.
Произведение lds равно площади dS, заметанной проводником при движении, а величина BdScosα равна потоку магнитной индукции dФ через эту площадь. Следовательно, можем написать:
dA=IdФ.
Рассматривая отрезок проводника с током как часть замкнутого контура и интегрируя это соотношение, найдем работу при перемещении контура с током в магнитном поле:
A = I(Ф2 — Ф1)
где Ф1 и Ф2 обозначают поток индукции магнитного поля через площадь контура соответственно в начальном и конечном положениях.
