Лекции для студентов

Электричество и магнетизм. Часть 2

3.3. Примеры вычисления магнитных полей с помощью закона Био-Савара-Лапласа.

1) Напряженность магнитного поля в центре кругового витка с током.

В данном случае имеем, согласно закону Био-Савара-Лапласа (рис.8.6):

,

откуда находим после интегрирования по всей длине витка — окружности радиуса R:

.

.

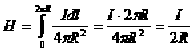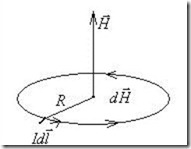
Рис.8.6. Магнитное поле в центре кругового витка с током.

2) Отрезок проводника с током конечной длины и бесконечно длинный проводник с током

В этом случае имеем (рис.8.7):

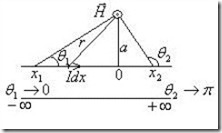
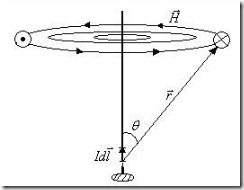
Рис.8.7. Магнитное поле прямолинейного проводника с током.

,

где

, , ,

тогда

.

Интегрируя это выражение в пределах от – x₁ до x₂ , находим:

где .

Переходя в этой формуле к пределу при и , получим формулу для расчета напряженности магнитного поля прямолинейного проводника с током бесконечной длины:

.

3) Магнитное поле движущегося заряда.

Любой проводник с током создает в окружающем пространстве магнитное поле. Но ток в проводнике — есть направленное движение зарядов. Следовательно, можно допустить, что источником магнитного поля являются движущиеся заряды. Тогда магнитное поле, созданное проводником с током в некоторой точке пространства, будет представлять собой суперпозицию магнитных полей, созданных в этой же точке пространства каждым из движущихся зарядов в отдельности.

Пусть – скорость упорядоченного движения зарядов в проводнике; q – заряд носителя тока (в металлах q = — e). Для элемента тока можем написать:

dNq,

где n = dN/dV — концентрация зарядов, dN – число зарядов в элементе объема dV = Sdl.

На основании закона Био-Савара-Лапласа, напряженность магнитного поля, созданного одним движущимся зарядом, будет:

или в векторном виде

.

Эта формула отражает релятивистскую (относительную) сущность магнитного поля. Она показывает, что магнитное поле проявляется как результат относительного движения заряда. Отметим, что приведенная формула справедлива при скоростях движения заряда (с=3∙10⁸ м/с — скорость света в вакууме).