Лекции для студентов

Физика полупроводников. Лекция 1

§6. Связь между структурами прямой и обратной решеткой кристалла.

Сначала рассмотрим скалярное произведение собственного вектора прямой решетки и собственного вектора обратной решетки одного и того же кристалла, и учитывая что скалярное произведение их базисных векторов , получим:

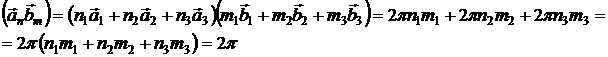(1)

С другой стороны

(2)

,

Из (2) следует что

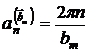(3).

Если считать, что n = const, то проекция (3) определяет собой кристаллографическую плоскость перпендикулярную и отстающую от начальных координат на величину (3).

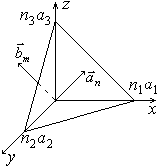
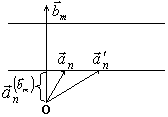Кристаллографическая плоскость — это такая плоскость, на которой находится бесконечное множество узлов кристаллической решетки. Из рисунка видно, что конец вектора лежит на плоскости (n), таким образом, на этой плоскости имеется хотя бы один узел. Покажем, что если имеется на этой плоскости хотя бы один узел (конец вектора ), то на этой плоскости имеется бесконечное множество других узлов, а это означает что плоскость кристаллографическая. Действительно, наряду с вектором рассмотрим множество собственных векторов:

, N — любое целое число, .

Покажем, что вектора дают с вектором такое же скалярное произведение, что и с вектором .

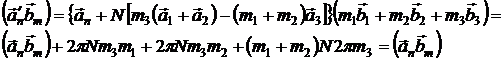
Отсюда следует, что концы векторов также лежат на плоскости на которой лежит конец вектора , значит плоскость перпендикулярная вектору и отстоящая от начальных координат на величину (3) является кристаллографической. Так как N — любое целое число, то вектору соответствует семейство параллельных плоскостей перпендикулярных вектору . Например, числу n+1 будет соответствовать другая плоскость перпендикулярная вектору , которая отстоит от начала координат на величину 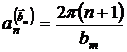. 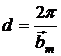Расстояние между соседними кристаллографическими плоскостями перпендикулярные вектору , очевидно равно (4).

Используя вышеприведенные выводы для следующего: покажем, что кристаллографическая плоскость перпендикулярная вектору имеет индексы Миллера (hkl) пропорциональные числам m₁, m₂, m₃.

Предположим, что кристаллографическая плоскость пересекает оси координат в точках с координатами: , , . Пусть  — собственный вектор, конец которого лежит на этой плоскости. Вектора  — собственные вектора прямой решетки концы, которых лежат на данной кристаллографической плоскости. (n₁, n₂, n₃ — целые числа). Обозначим через собственный вектор обратной решетки перпендикулярный данной кристаллографической плоскости. Этот вектор дает одинаковое скалярное произведение с вектором и с векторами :

(5)

С другой стороны

; ; . (6)

Из (5) и (6) следует, что

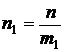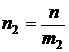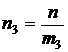; ; . (7)

Из (7) следует, что

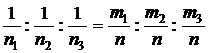(8)

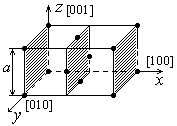Из (8) получаем, что индексы Миллера данной кристаллографической плоскости кратны числам m₁, m₂, m₃. После сокращения на общий множитель получаем истинные индексы Миллера. Используя вышеприведенные данные, найдем тип обратной решетки для данного типа прямой решетки. Предположим, что прямая решетка является кубической гранецентрированной. На рисунке заштрихованы кристаллографические плоскости перпендикулярные оси [011]. Расстояние между рассмотренными кристаллографическими плоскостями 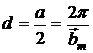, , . Также можно найти вектора , которые параллельны двум другим ребрам и равные . Вектора перпендикулярные друг другу, поэтому по этому обратная решетка кубическая. Плоскости гранецентрированного куба перпендикулярны диагоналям куба и кристаллографические плоскости перпендикулярные диагоналям куба отстоят друг от друга на 1/3 часть диагонали куба. 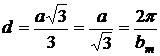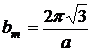, ,  — параллелен главной диагонали куба, так как он перпендикулярен плоскостям . Диагональ куба обратной решетки равна .

Видно, что 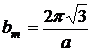по величине в два раза меньше диагонали куба обратной решетки, значит, конец этого вектора приходится на центр куба, т.е. в центре куба обратной решетки имеется узел. Значит, обратная решетка для кристаллов кубической гранецентрированной системы является кубической объемно-центрированной и наоборот.