Физика полупроводников. Лекция 1
- Физика полупроводников. Лекция 1
- Глава I. Структура полупроводниковых кристаллов
- §1.2. Элементы симметрии кристаллов.
- §2.1. Оси симметрии.
- §2.2. Плоскости симметрии.
- §2.3. Зеркально — поворотные оси симметрии.
- §3. Типы простых кристаллических решеток.
- §4. Кристаллографические индексы Миллера.
- §5. Обратная решетка кристалла и ее ячейка Вигнерра — Зейтца. .
- §6. Связь между структурами прямой и обратной решеткой кристалла.
- §7. Построение зон Бриллюэна для каждой из некоторых типов кристаллических решеток.
- 7.2 Кубическая гранецентрированная решетка.
- 7.3. Гексагональная решетка.
- 7.4. Кристаллы графита.
- §8. Структура основных типов полупроводниковых кристаллов.
- §9. Неупорядоченные (некристаллические полупроводники).
- §10. Типы и структура жидких кристаллов.
- §11.Жидко кристаллические приборы для отображения информации.
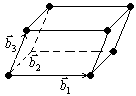
Для каждой прямой решетки кристалла можно построить ей обратную. Обратные решетки широко используются в зонной теории твердых тел при описании движения электронов проводимости и фотонов. Пусть прямая решетки кристалла характеризуется базисными векторами ![]() и собственными векторами
и собственными векторами ![]() . Обозначим через
. Обозначим через ![]() базисные вектора обратной решетки кристалла. Свяжем базисные вектора прямой и обратной решетки кристалла условием, что скалярное произведение:
базисные вектора обратной решетки кристалла. Свяжем базисные вектора прямой и обратной решетки кристалла условием, что скалярное произведение:
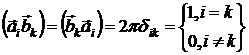 ;
; ![]() (1)
(1)
Условию (1) удовлетворяет следующие вектора:
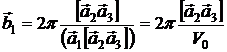 ;
;
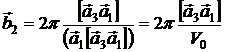 ; (2)
; (2)
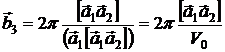 .
.
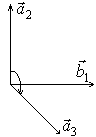 Видно что,
Видно что, ![]() ,
, ![]() ,
, ![]() , значит
, значит ![]() ,
, ![]() , также
, также ![]() и
и ![]() , т.е.
, т.е. ![]() перпендикулярна двум базисным векторам прямой решетки, индексы которых отличаются от j. Видно, что тройка векторов
перпендикулярна двум базисным векторам прямой решетки, индексы которых отличаются от j. Видно, что тройка векторов ![]() образуют правовинтовые системы, если
образуют правовинтовые системы, если ![]() и
и ![]() . На основе векторов
. На основе векторов ![]() построим бесконечную совокупность векторов
построим бесконечную совокупность векторов ![]() (3); где
(3); где ![]() , т.е.
, т.е. ![]() представляют собой целочисленную комбинацию векторов
представляют собой целочисленную комбинацию векторов ![]() , они имеют размерность что и базисные вектора, а базисные вектора имеют размерность обратную длине, иными словами
, они имеют размерность что и базисные вектора, а базисные вектора имеют размерность обратную длине, иными словами ![]() лежат в обратном пространстве. Будем откладывать с какой-нибудь точки — вектора
лежат в обратном пространстве. Будем откладывать с какой-нибудь точки — вектора ![]() Концы таких векторов образуют узлы обратной решетки, а совокупность узлов есть обратная решетка кристалла. Если
Концы таких векторов образуют узлы обратной решетки, а совокупность узлов есть обратная решетка кристалла. Если ![]() назывались собственными векторами прямой решетки, то
назывались собственными векторами прямой решетки, то ![]() являются собственными векторами обратной решетки. Ячейка построенная на базисных векторах
являются собственными векторами обратной решетки. Ячейка построенная на базисных векторах ![]() называется элементарной ячейкой обратной решетки, ее объем равен
называется элементарной ячейкой обратной решетки, ее объем равен 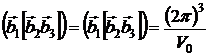 .
.
Бесконечным повторением в обратном пространстве элементарной ячейки можно получить всю бесконечную обратную решетку. На одну элементарную ячейку приходится один узел, следовательно число ячеек образующих обратную решетку равно числу ее узлов. 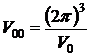 ;
; ![]() . Элементарную ячейку обратной решетки можно получить иначе. Для этого возьмем какой-нибудь узел (Г) обратной решетки за начало отсчета. Проведем из этого узла (Г) прямые линии в ближайшие соседние узлы через середины этих перпендикулярно к ним проведем плоскости. Многогранник, полученный в результате пересечения плоскостей называется ячейкой Вигнера-Зейца. Возле каждого узла обратной решетки можно построить такую ячейку, при этом исходя из условия построения ячейки Вигнера-Зейца они не будут пересекаться и заполнят весь объем обратного пространства. Следовательно, объем ячейки Вигнера-Зейца равен объему параллелепипеда построенного на векторах
. Элементарную ячейку обратной решетки можно получить иначе. Для этого возьмем какой-нибудь узел (Г) обратной решетки за начало отсчета. Проведем из этого узла (Г) прямые линии в ближайшие соседние узлы через середины этих перпендикулярно к ним проведем плоскости. Многогранник, полученный в результате пересечения плоскостей называется ячейкой Вигнера-Зейца. Возле каждого узла обратной решетки можно построить такую ячейку, при этом исходя из условия построения ячейки Вигнера-Зейца они не будут пересекаться и заполнят весь объем обратного пространства. Следовательно, объем ячейки Вигнера-Зейца равен объему параллелепипеда построенного на векторах ![]() . Ячейка Вигнера-Зейца повторяет симметрию обратной решетки, в то время как параллелепипед, построенный на векторах
. Ячейка Вигнера-Зейца повторяет симметрию обратной решетки, в то время как параллелепипед, построенный на векторах ![]() не обладает симметрией обратной решетки.
не обладает симметрией обратной решетки.
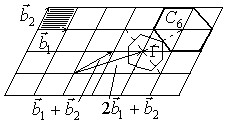 |
Рассмотрим пример: Пусть обратная решетка построена на базисных векторах, удовлетворяет условию
Заштрихована элементарная ячейка обратной решетки.
 Видно, что обратная решетка имеет ось симметрии 6-го порядка. С другой стороны как видно ячейка Вигнера-Зейца представляет собой правильный шести угольник. В то время как элементарная ячейка построенная на векторах
Видно, что обратная решетка имеет ось симметрии 6-го порядка. С другой стороны как видно ячейка Вигнера-Зейца представляет собой правильный шести угольник. В то время как элементарная ячейка построенная на векторах ![]() не обладает такой симметрией. Будем обозначать вектора, проводимые из центра ячейки Вигнера-Зейца в любую ячейку через
не обладает такой симметрией. Будем обозначать вектора, проводимые из центра ячейки Вигнера-Зейца в любую ячейку через ![]() , они имеют размерность обратную длине. Два вектора
, они имеют размерность обратную длине. Два вектора ![]() и
и ![]() будем называть взаимно эквивалентными, если они отличаются друг от друга на какой-нибудь собственный вектор обратной решетки, т.е. если
будем называть взаимно эквивалентными, если они отличаются друг от друга на какой-нибудь собственный вектор обратной решетки, т.е. если ![]()
![]() . По условию построения ячейки Вигнера-Зейца внутри нее нет взаимно эквивалентных векторов
. По условию построения ячейки Вигнера-Зейца внутри нее нет взаимно эквивалентных векторов ![]() . Эквивалентные вектора имеются только на границе ячейки Вигнера-Зейца:
. Эквивалентные вектора имеются только на границе ячейки Вигнера-Зейца:
![]() ;
; ![]() ;
; ![]() .
.
Любые два вектора принадлежащие ячейке Вигнера-Зейца отличаются друг от друга не более чем на вектор ![]() , таким образом, внутри себя ячейка Вигнера-Зейца содержит бесконечную совокупность неэквивалентных векторов. Совокупность неэквивалентных векторов образуют в обратном пространстве область, которая называется первой зоной Бриллюэна. Следовательно, первая зона Бриллюэна совпадает с ячейкой Вигнера-Зейца обратной решетки. Значит, первой зоне Бриллюэна принадлежат вектора
, таким образом, внутри себя ячейка Вигнера-Зейца содержит бесконечную совокупность неэквивалентных векторов. Совокупность неэквивалентных векторов образуют в обратном пространстве область, которая называется первой зоной Бриллюэна. Следовательно, первая зона Бриллюэна совпадает с ячейкой Вигнера-Зейца обратной решетки. Значит, первой зоне Бриллюэна принадлежат вектора ![]() , которые короче всех эквивалентных векторов обратного пространства.
, которые короче всех эквивалентных векторов обратного пространства.
Докажем, что первой зоне Бриллюэна принадлежат вектора ![]() , которые удовлетворяют неравенству:
, которые удовлетворяют неравенству: ![]() ,
, ![]() .
.
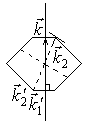
Доказательство: Исходя из построений ячейки Вигнера-Зейца, должно выполняться следующие неравенство:
![]() (1)
(1)
где ![]() модуль проекции вектора
модуль проекции вектора ![]() :
: 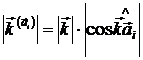 ,
, ![]() — модуль проекции вектора
— модуль проекции вектора ![]() ,
, ![]() — собственные вектора проведенные в ближайшие к Г узлы. Очевидно (1) не измениться, если его правую часть умножить на модуль
— собственные вектора проведенные в ближайшие к Г узлы. Очевидно (1) не измениться, если его правую часть умножить на модуль ![]() , тогда получаем:
, тогда получаем:
![]() (2)
(2)
![]() (3)
(3)
![]()
![]() (4)
(4)
Для выполнения неравенства (3) в ряду ![]() мы должны взять целое наименьшее число больше 0, то есть +1, тогда (3) примет вид:
мы должны взять целое наименьшее число больше 0, то есть +1, тогда (3) примет вид:
![]() (4)
(4) ![]() (5)
(5)
Если из точки Г провести прямые линии в следующие за ближайшими узлами узлы и через середины их провести перпендикулярные плоскости, то получим многогранник, если из него вычесть объем первой зоны Бриллюэна, то оставшийся объем образует вторую зону Бриллюэна и т.д. Для примера рассмотрим кристалл с плоской квадратной решеткой: а1 = а2 = а; ![]() . Базисные вектора обратной решетки есть
. Базисные вектора обратной решетки есть ![]() , и
, и ![]() , значит обратная решетка плоской квадратной решетки является тоже квадратной.
, значит обратная решетка плоской квадратной решетки является тоже квадратной.
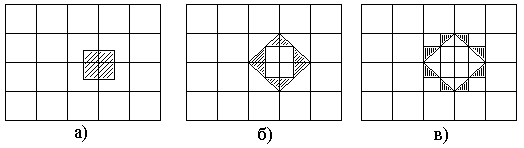 |
На рисунке (а) заштрихована первая зона Бриллюэна, на рисунке (б) заштрихована вторая зона Бриллюэна, на рисунке (в) заштрихована третья зона Бриллюэна.
