Физика полупроводников. Лекция 1
- Физика полупроводников. Лекция 1
- Глава I. Структура полупроводниковых кристаллов
- §1.2. Элементы симметрии кристаллов.
- §2.1. Оси симметрии.
- §2.2. Плоскости симметрии.
- §2.3. Зеркально — поворотные оси симметрии.
- §3. Типы простых кристаллических решеток.
- §4. Кристаллографические индексы Миллера.
- §5. Обратная решетка кристалла и ее ячейка Вигнерра — Зейтца. .
- §6. Связь между структурами прямой и обратной решеткой кристалла.
- §7. Построение зон Бриллюэна для каждой из некоторых типов кристаллических решеток.
- 7.2 Кубическая гранецентрированная решетка.
- 7.3. Гексагональная решетка.
- 7.4. Кристаллы графита.
- §8. Структура основных типов полупроводниковых кристаллов.
- §9. Неупорядоченные (некристаллические полупроводники).
- §10. Типы и структура жидких кристаллов.
- §11.Жидко кристаллические приборы для отображения информации.
Прямая решетка кристалла характеризуется базисом 
, а обратная решетка базисом 
. Помимо базисных векторов введем ортогональную систему координат определяемую ортами i, j, k, при этом одну и ту же систему координат будем использовать как для прямой, так и для обратной решетки. Построим первые зоны Бриллюэна для таких типов кристаллических решеток, которые в основном определяют структуру кристаллических классов.
1. Простая кубическая решетка.
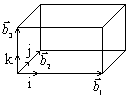
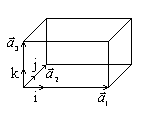Ее можно получить повторением в пространстве базисной ячейки куба со стороной а. В этом случае в качестве базиса удобно принять вектора 
обладающие свойством а1 = а2 = а3, α = β = γ = 900. Направим орты i, j, k вдоль ребер куба. Базис прямой решетки будет иметь вид:
,
,
.
|
[…] |
|
|
|
|
|
0 |
|
- |
|
|
- |
0 |
|
|
|
|
- |
0 |
Найдем базис обратной решетки:
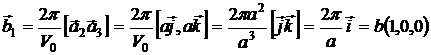
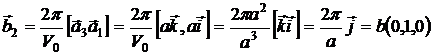
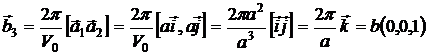
Ячейка, построенная на векторах 
— это базисная ячейка обратной решетки, куб ребра которого направлены вдоль ортов. Объем этой ячейки будет совпадать с объемом первой зоны Бриллюэна.
.
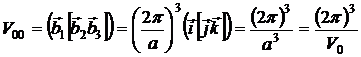Обратную решетку можно получить повторением в пространстве базисной ячейки простого куба со стороной 
. Первую зону Бриллюэна будем находить как многогранник, построенный по известному правилу с центром в точке γ = Г. Для этого с какого-нибудь узла γ = Г проведем прямые отрезки в ближайшие узлы, через середины этих отрезков проведем плоскости. Получим многогранник со стороной 
(куб). Значит, первая зона Бриллюэна кристалла с простой кубической решеткой есть куб со стороной 
. Центр куба (γ = Г) будем принимать за начало отсчета, т.е. ей соответствует вектор 
.
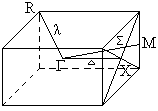На рисунке приведена зона Бриллюэна кристалла с простой кубической решеткой, на ней отмечены симметричные линии и симметричные точки. Симметричные линии (λ, Σ, Δ) проходят вдоль направлений , , соответственно. Число линий λ = 8, Σ = 12, Δ = 6. Число симметричных точек R = 8 M = 12 и X = 6. Точки R имеют координаты типа 
. Точки X имеют координаты типа 
. Точки M имеют координаты типа 
.
