Лекции для студентов

Физика полупроводников. Лекция 1

Ось симметрии это прямая, повороты вокруг которой совмещают кристалл сам с собой. Оси характеризуются своим порядком n. Порядок n это число совмещений кристалла при его повороте вокруг оси на 360⁰ . φ — наименьший угол поворота, при котором кристалл совмещается сам с собой. Если кристалл совмещается при повороте на угол φ, то он будет совмещаться при последовательном m — кратном повторении операции поворота на угол φ. Если порядок оси n, то с ней связаны повороты на углы . Оси симметрии n-го порядка будем обозначать через C_n в отличие от поворотов . .

Примеры осей симметрии в кристаллах.

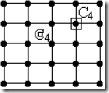Пример1: Бесконечная квадратная простая кристаллическая решетка имеет бесконечное число осей симметрии 4-го порядка. Все эти оси 4-го порядка эквивалентны, поэтому говорят, что он имеет одну ось симметрии 4-го порядка.

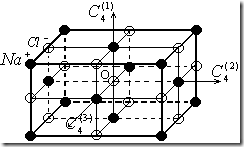
Пример2: Кристаллы (NaCl) имеют три взаимно перпендикулярные оси 4-го порядка . На рисунке приведен фрагмент кристаллической решетки NaCl. Видно, что кристалл NaCl состоит из двух кубических гранецентрированных простых решеток, примитивная решетка ромбоэдрическая. На одну примитивную ячейку приходится 2 атома (один белый другой черный).

Докажем теорему, что кристаллы имеют оси симметрии только порядка n = 1, 2, 3, 4, 6 (кристаллы не могут иметь 5, 7 и более высоких порядков, это относится и к зеркально — поворотным осям симметрии).

Доказательство: представим себе, что кристаллы имеют ось симметрии малого порядка. С этой осью связаны повороты на углы:

Видно, что вращения есть повороты на один и тот же угол в противоположных направлениях. Пусть ось Сn перпендикулярна плоскости рисунка и проходит через точку О, и пусть наименьший собственный вектор кристалла перпендикулярной оси Сn. являются преобразованиями симметрии кристаллов и следовательно они совмещают все эквивалентные точки кристалла, т.е. они переводят узлы решетки Бравэ в другие узлы этой же решетки. Переводят вектора в другие вектора этого же множества ( — комбинация базисных векторов ).

Подействуем на вектор преобразованиями и получим вектора:

, , ; ;

; ; , (целое число), потому что наименьший собственный вектор в выбранном направлении ; ; ;

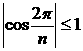Подставляя найденные значения α в выражение , находим что .