Физика полупроводников. Лекция 1
- Физика полупроводников. Лекция 1
- Глава I. Структура полупроводниковых кристаллов
- §1.2. Элементы симметрии кристаллов.
- §2.1. Оси симметрии.
- §2.2. Плоскости симметрии.
- §2.3. Зеркально — поворотные оси симметрии.
- §3. Типы простых кристаллических решеток.
- §4. Кристаллографические индексы Миллера.
- §5. Обратная решетка кристалла и ее ячейка Вигнерра — Зейтца. .
- §6. Связь между структурами прямой и обратной решеткой кристалла.
- §7. Построение зон Бриллюэна для каждой из некоторых типов кристаллических решеток.
- 7.2 Кубическая гранецентрированная решетка.
- 7.3. Гексагональная решетка.
- 7.4. Кристаллы графита.
- §8. Структура основных типов полупроводниковых кристаллов.
- §9. Неупорядоченные (некристаллические полупроводники).
- §10. Типы и структура жидких кристаллов.
- §11.Жидко кристаллические приборы для отображения информации.
Плоскость симметрии — это такая плоскость, когда кристалл совмещается сам с собой, если все его точки одной части перенести за плоскость по перпендикуляру на равные расстояния.
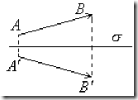 Подействуем преобразованием
Подействуем преобразованием ![]() на вектор
на вектор ![]() , получим:
, получим: ![]() . Если плоскость σ перпендикулярна оси Сn, то плоскость обозначается σh, если плоскость σ проходит через ось Сn, то плоскость обозначается σv.
. Если плоскость σ перпендикулярна оси Сn, то плоскость обозначается σh, если плоскость σ проходит через ось Сn, то плоскость обозначается σv.
Теорема: Если кристаллы имеют оси симметрии порядка n≥3 (3,4,6), то они имеют и плоскости симметрии σv проходящие через эти оси.
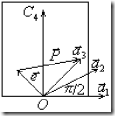 Доказательство: Докажем эту теорему только для оси
Доказательство: Докажем эту теорему только для оси ![]() , с ней связаны повороты
, с ней связаны повороты ![]() . Пусть
. Пусть ![]() наименьший собственный вектор перпендикулярный оси С4. Подействуем на
наименьший собственный вектор перпендикулярный оси С4. Подействуем на ![]() преобразованием
преобразованием ![]() , получим:
, получим: ![]()
![]() . Вектор
. Вектор ![]() является наименьшим собственным вектором в своем направлении. Проведем через ось С4 и
является наименьшим собственным вектором в своем направлении. Проведем через ось С4 и ![]() плоскость σv. Покажем, что эта плоскость будет являться плоскостью симметрии данного кристалла. Для этого надо знать, что любое преобразование α являлось преобразованием симметрии, если выполняется следующие условие:
плоскость σv. Покажем, что эта плоскость будет являться плоскостью симметрии данного кристалла. Для этого надо знать, что любое преобразование α являлось преобразованием симметрии, если выполняется следующие условие:
![]() ;
; ![]() ;
; ![]() . Подействуем операцией σv на
. Подействуем операцией σv на ![]() , получим:
, получим:
![]() ;
; ![]() ,
, ![]() — третий базисный вектор кристалла. Введем вектор
— третий базисный вектор кристалла. Введем вектор ![]() перпендикулярный оси С4,
перпендикулярный оси С4, ![]() .
.
![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() плоскости в которой лежат вектора
плоскости в которой лежат вектора ![]() и
и ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
Следовательно, плоскость ![]()
![]() , проходящая через оси симметрии четвертого порядка, является плоскостью симметрии кристалла. Например, кристаллы NaCl имеют три взаимно перпендикулярные плоскости симметрии, в которых, в соответствии с доказанной теоремой лежат оси симметрии четвертого порядка.
, проходящая через оси симметрии четвертого порядка, является плоскостью симметрии кристалла. Например, кристаллы NaCl имеют три взаимно перпендикулярные плоскости симметрии, в которых, в соответствии с доказанной теоремой лежат оси симметрии четвертого порядка.
