Физика полупроводников. Лекция 1
- Физика полупроводников. Лекция 1
- Глава I. Структура полупроводниковых кристаллов
- §1.2. Элементы симметрии кристаллов.
- §2.1. Оси симметрии.
- §2.2. Плоскости симметрии.
- §2.3. Зеркально — поворотные оси симметрии.
- §3. Типы простых кристаллических решеток.
- §4. Кристаллографические индексы Миллера.
- §5. Обратная решетка кристалла и ее ячейка Вигнерра — Зейтца. .
- §6. Связь между структурами прямой и обратной решеткой кристалла.
- §7. Построение зон Бриллюэна для каждой из некоторых типов кристаллических решеток.
- 7.2 Кубическая гранецентрированная решетка.
- 7.3. Гексагональная решетка.
- 7.4. Кристаллы графита.
- §8. Структура основных типов полупроводниковых кристаллов.
- §9. Неупорядоченные (некристаллические полупроводники).
- §10. Типы и структура жидких кристаллов.
- §11.Жидко кристаллические приборы для отображения информации.
Ее базисной ячейкой построенной на векторах ![]() , является прямая призма, в основании которой лежит ромб. Один из углов которого равен 1200. а1 = а2 = а, а3 = с,
, является прямая призма, в основании которой лежит ромб. Один из углов которого равен 1200. а1 = а2 = а, а3 = с, ![]() ,
, ![]() ,
, ![]() .
.
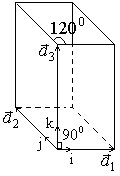
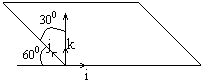 Выразим базис решетки через орты:
Выразим базис решетки через орты:
![]()
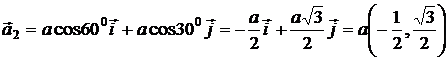
![]() .
.
Найдем объем обратной решетки:
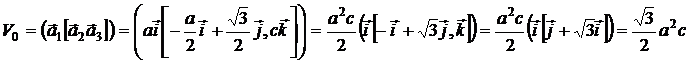 Найдем базис обратной решетки:
Найдем базис обратной решетки:
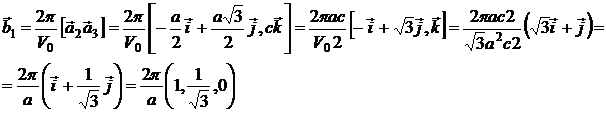
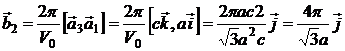
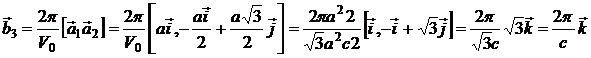
Заметим, что ![]() ,
, ![]() . Найдем модули векторов
. Найдем модули векторов ![]() .
.
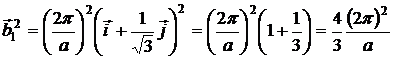 ,
, 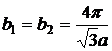
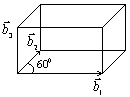 Базисной ячейкой обратной решетки является призма, в основании которой лежит ромб.
Базисной ячейкой обратной решетки является призма, в основании которой лежит ромб.
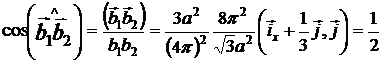 ,
, ![]()
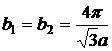 ,
, ![]() .
.
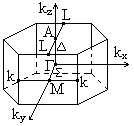 Повторением в пространстве такой базисной ячейки можно получить всю обратную решетку. Как видно обратная решетка для гексагональной системы является также гексагональной. По известному правилу выделим многогранник симметричный относительно точки Г, который будет представлять первую зону Бриллюэна для кристаллической решетки гексагонального типа — шестигранная призма, на которой указаны симметричны точки и симметричные линии. Найдем объем зоны Бриллюэна.
Повторением в пространстве такой базисной ячейки можно получить всю обратную решетку. Как видно обратная решетка для гексагональной системы является также гексагональной. По известному правилу выделим многогранник симметричный относительно точки Г, который будет представлять первую зону Бриллюэна для кристаллической решетки гексагонального типа — шестигранная призма, на которой указаны симметричны точки и симметричные линии. Найдем объем зоны Бриллюэна.