Физика полупроводников. Лекция 1
- Физика полупроводников. Лекция 1
- Глава I. Структура полупроводниковых кристаллов
- §1.2. Элементы симметрии кристаллов.
- §2.1. Оси симметрии.
- §2.2. Плоскости симметрии.
- §2.3. Зеркально — поворотные оси симметрии.
- §3. Типы простых кристаллических решеток.
- §4. Кристаллографические индексы Миллера.
- §5. Обратная решетка кристалла и ее ячейка Вигнерра — Зейтца. .
- §6. Связь между структурами прямой и обратной решеткой кристалла.
- §7. Построение зон Бриллюэна для каждой из некоторых типов кристаллических решеток.
- 7.2 Кубическая гранецентрированная решетка.
- 7.3. Гексагональная решетка.
- 7.4. Кристаллы графита.
- §8. Структура основных типов полупроводниковых кристаллов.
- §9. Неупорядоченные (некристаллические полупроводники).
- §10. Типы и структура жидких кристаллов.
- §11.Жидко кристаллические приборы для отображения информации.
Структура простых кристаллических решеток совпадает со структурой своих решеток Бравэ. Сложные кристаллические решетки можно представить в виде системы S простых кристаллических решеток, сдвинутых одна относительно другой определенным образом. Используя три правила отбора, найдем все типы решеток Бравэ, т.е. все типы простых кристаллических решеток:
1. Кристаллы должны иметь оси n≥3 (3,4,6).
2. Кристаллы должны иметь плоскости симметрии σv.
3. Решетки Бравэ принадлежат трансляционному множеству 
, в котором для каждого вектора 
имеется ему обратный вектор 
. А точечным преобразованием переводящим вектор 
в вектор 
является операция инверсии, значит, любая решетка Бравэ имеет центр симметрии.
Существует всего 14 типов кристаллических решеток, распределенных по семи системам (сингониям): триклинная, моноклинная, ортогональная, тетрагональная, ромбоэдрическая, гексагональная, кубическая.
1. 
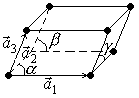Триклинная примитивная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами 
, углы между которыми: 
; 
; 
; 
, и у которой атомы расположены только в вершинах элементарной ячейки.
2. 
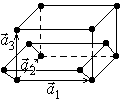
Моноклинная примитивная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами 
, углы между которыми: 
; 
, и у которой атомы расположены только в вершинах элементарной ячейки.
3. Моноклинная базоцентрированная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами 
, углы между которыми: 
; 
, и у которой атомы расположены в вершинах ячейки и в центре двух противоположных, прямоугольных гранях.
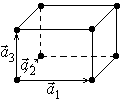
4. Ортогональная примитивная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами 
, углы между которыми: 
, и у которой атомы расположены только в вершинах элементарной ячейки.
5. Ортогональная базоцентрированная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами 
, углы между которыми: 
, и у которой атомы расположены в вершинах ячейки и в центре двух противоположных гранях.
6. 
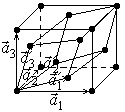Ортогональная гранецентрированная решетка, которую можно получить повторением в пространстве ячейки с ребрами 
, углы между которыми: 
, и у которой атомы расположены в вершинах ячейки и в центрах всех шести гранях. Примитивной будет являться ячейка построенная на векторах 
. Повторением такой решетки можно получить всю ортогональную гранецентрированную решетку.
7. 
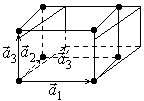Ортогональная объемноцентрированная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами 
, углы между которыми: 
, и у которой атомы расположены в вершинах ячейки и в центре решетки. 
проеден к узлу в центре решетки. Примитивной будет являться ячейка построенная на векторах 
.
8. Тетрагональная примитивная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами 
, углы между которыми: 
, и у которой атомы расположены только в вершинах элементарной ячейки.
9. 
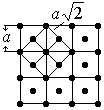Тетрагональная объемноцентрированная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами 
, углы между которыми: 
, и у которой атомы расположены в вершинах и в центре ячейки. Центрирование граней ячеек не приведет к новому типу кристаллических решеток.
10. Ромбоэдрическая примитивная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами 
, углы между которыми: 
, и у которой атомы расположены только в вершинах элементарной ячейки.
11. 
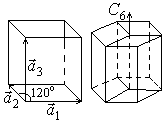Гексагональная примитивная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами 
, углы между которыми: 
; 
,и у которой атомы расположены только в вершинах элементарной ячейки. Часто элементарные ячейки представляют в виде шестигранной призмы, которая состоит из трех четырехгранных призм, в частности ось симметрии шестого порядка.
12. Кубическая примитивная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами 
, углы между которыми: 
, и у которой атомы расположены только в вершинах элементарной ячейки.
13. Кубическая гранецентрированная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами 
, углы между которыми: 
, и у которой атомы расположены в вершинах и в центрах всех шести гранях ячейки. Примитивная ячейка — ромбоэдрическая.
14. Кубическая примитивная решетка, которую можно получить повторением в пространстве элементарной ячейки с ребрами 
, углы между которыми: 
, и у которой атомы расположены в вершинах и в центре ячейки.
Кристаллические структуры сложных кристаллов состоят из систем одной из 14-ти типов простых решеток.
