Физика полупроводников. Лекция 1
- Физика полупроводников. Лекция 1
- Глава I. Структура полупроводниковых кристаллов
- §1.2. Элементы симметрии кристаллов.
- §2.1. Оси симметрии.
- §2.2. Плоскости симметрии.
- §2.3. Зеркально — поворотные оси симметрии.
- §3. Типы простых кристаллических решеток.
- §4. Кристаллографические индексы Миллера.
- §5. Обратная решетка кристалла и ее ячейка Вигнерра — Зейтца. .
- §6. Связь между структурами прямой и обратной решеткой кристалла.
- §7. Построение зон Бриллюэна для каждой из некоторых типов кристаллических решеток.
- 7.2 Кубическая гранецентрированная решетка.
- 7.3. Гексагональная решетка.
- 7.4. Кристаллы графита.
- §8. Структура основных типов полупроводниковых кристаллов.
- §9. Неупорядоченные (некристаллические полупроводники).
- §10. Типы и структура жидких кристаллов.
- §11.Жидко кристаллические приборы для отображения информации.
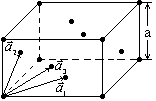
Ее можно получить повторением в пространстве гранецентрированной ячейки. Проведем орты вдоль ребер куба. Базис прямой решетки будет иметь вид:
Найдем объем базисной ячейки:
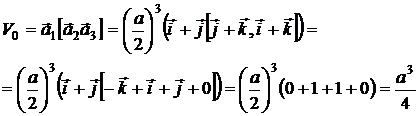
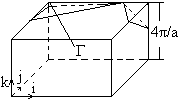
В параграфе 6 нами показано, что обратной решеткой для кубической гранецентрированной решетки является кубическая объемно-центрированная с ребром куба 
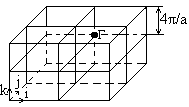
. Повторением в пространстве объемно-центрированного куба можно получить всю обратную решетку. Для построения первой зоны Бриллюэна используем правило построения многогранника симметричного относительно точки Г, за начало отсчета возьмем любой узел обратной решетки, например центр куба. Построим многогранник симметричный относительно точки Г, для этого из точки Г, проведем отрезки в ближайшие узлы: 6 отрезков соединяющих точку Г с центрами соседних кубов, они направлены вдоль ортов i, j, k, и 8 отрезков соединяющих точку Г с вершинами куба. Сначала проведем плоскости через середины первых шести отрезков и получим многогранник — куб со стороной 
. Теперь проведем плоскости через середины восьми других отрезков. Эти плоскости перпендикулярны направлениям [111]. При отсечении одной вершины куба получается в сечении треугольная грань. Но эту грань пересекают еще три другие плоскости отсекающие соседние вершины. В результате таких пересечений каждая треугольная грань превращается в правильный шести угольник. Зона Бриллюэна кристалла с гранецентрированной решеткой –представляет собой четырнадцати угольник, который получил название усеченного октаэдра. В этом многограннике шесть граней квадраты, плоскости которых перпендикулярны направлениям ортов и восемь граней правильные шести угольники, плоскости которых перпендикулярны осям . На рисунке показана зона Бриллюэна кристаллов с гранецентрированной решеткой: Ge, Si, A2B6 (ZnTe, CdTe, ZnSe, HgTe), A3B5 (GaAs …)
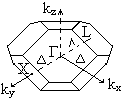Симметричные линии Δ (6), Λ (8) направлены вдоль осей типа и соответственно. Линии Δ направлены вдоль ортов i, j, k, точки Х (6) и L (8) являются предельным положением линий Δ и Λ; точки Х имеют координаты 
, а точки L имеют координаты 
.
Найдем, на каком расстоянии расположены точки L от центра куба, учтем что вектор 
. Для этого найдем квадрат этого вектора:
, 
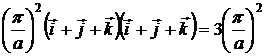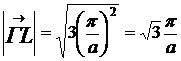
Объем зоны Бриллюэна равной объему ячейки Вигнера — Зейца.
.
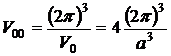