Лекции для студентов

Физика полупроводников. Лекция 1

§1. Решетки Бравэ кристаллов. Простая и сложные кристаллические решетки.

Кристаллы основная форма существования твердых тел около 95% литосферы занимают кристаллы.

С микроскопической точки зрения кристаллы представляют собой дискретную структуру, состоящую из огромного числа атомов или молекул образующих в пространстве правильную периодическую структуру. Свойства пространственной периодичности означает, что для каждого кристалла можно указать 3 некомпланарных вектора таких что трансляция (параллельный перенос) кристалла на любой вектор , где совмещает кристалл сам с собой все физически эквивалентные точки кристалла. называются базисными (основными) векторами кристалла называются собственными векторами кристалла, они как видно представляют целочисленную комбинацию базисных векторов. Такие рассуждения верны только для кристаллов бесконечных размеров. При трансляции на вектор кристалла конечных размеров, края кристалла выходят за свои границы и, следовательно, кристалл не совмещается сам с собой. Мы также не учитываем тепловое колебание кристаллической решетки (адиабатическое приближение).

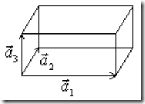
Будем откладывать из какой-нибудь точки кристалла вектор , за начало отсчета лучше выбрать центр какого-либо атома, тогда концы векторов образуют узлы (математическая абстракция). А совокупность узлов образует решетку Бравэ кристалла.

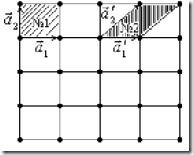Выбор базисных векторов, а следовательно и элементарных ячеек не однозначен, это можно видеть на примере двухмерной плоской кристаллической решетки. Обычно кристаллы характеризуют такой элементарной ячейкой, которая обладает свойствами: 1) Они наилучшим образом отражают симметрию кристалла. 2) Чтобы у ячейки были прямые углы. 3) Имела наименьший объем . Такая ячейка получила название примитивная ячейка. Для плоского кристалла ячейкой №1 можно характеризовать кристалл. Базисные вектора примитивных ячеек являются наименьшими в своих направлениях кристалла.

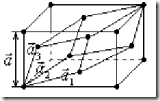В разных кристаллах число атомов приходящихся на одну примитивную ячейку может быть разным. Кристаллы, у которых на одну примитивную ячейку приходится один атом (S=1), называют простой. Приведенная на рисунке плоская решетка является примером простой решетки. В ее примитивной ячейке атомы расположены только в вершинах. При этом каждый атом принадлежит своей ячейке ¼ частью, следовательно, на одну примитивную ячейку приходится 4·¼=1 атом. Примером кристалла с простой решеткой служит металл, кристаллы Cu, Ag, Ni, Au, Pb… Все они кристаллизуются в кубическую гранецентрированную решетку (кгр), т.е. кристаллы таких металлов можно получить повторением в пространстве куба, атомы находятся в вершинах и в центре шести боковых гранях. На гранецентрированный куб приходится 8·1/8 + 1/2·6 = 4 атома. На первый взгляд кажется, что металлы имеют сложную решетку, однако гранецентрированный куб у таких кристаллов не является примитивной. Примитивной ячейкой является ромбоэдрическая (куб вытянутый вдоль главной диагонали), ячейку можно построить на базисных векторах . В этой ячейки атомы расположены только в ее вершинах, значит, на нее приходится 1/8·8 =1 атом. Значит, перечисленные металлы имеют простую кристаллическую решетку. Кристаллы с простой решеткой состоят из атомов только одного типа. Структура решетки Бравэ у простых кристаллов совпадает со структурой кристаллической решетки. Некоторые кристаллы, состоящие из атомов одного типа (Ge, Si), а также все кристаллы состоящие из атомов разного типа имеют сложную кристаллическую решетку: у них на одну примитивную ячейку приходится более одного атома (S≥2). Для примера приведем сложную плоскую решетку, состоящую из атомов одного типа.

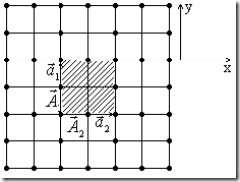Наименьшими базисными векторами в направлении х и у являются вектора и , модули которых занимают две клетки. Видно, что на примитивную ячейку приходится S = 4·1/4 + 1/2·4 = 3 атома. Значит, такой плоский кристалл, состоящий из атомов одного типа имеет сложную решетку (S = 3 атома).

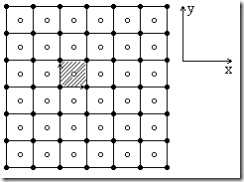На следующем рисунке приведен пример решетки, состоящей из атомов дух типов. Наименьшими собственными векторами такого кристалла в направлении осей х и у являются вектора и (наименьшие базисные вектора). Заштрихована примитивная ячейка кристалла, на нее приходится S = 1_о + 1_● = 2 атома. Такой кристалл имеет сложную решетку. Сложную решетку можно представить в виде системы простых решеток вдвинутых одна в другую определенным образом. Кристаллы характеризуются не только , но и векторами смещения .