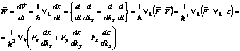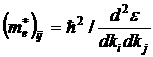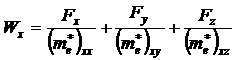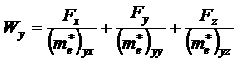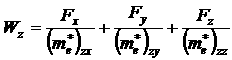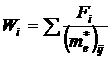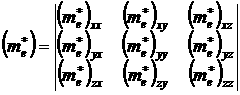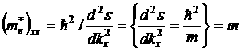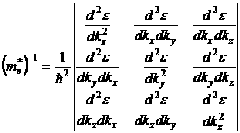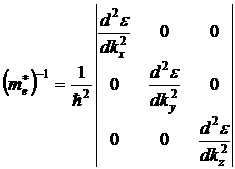Физика полупроводников. Лекция 2
- Физика полупроводников. Лекция 2
- §2. Адиабатическое приближение в квантовой теории твердых тел.
- §3. Одноэлектронное приближение в квантовой теории твердых тел.
- §4. Квантовая теория свободных электронов кристалла.
- §5. Волновая функция связанных электронов кристалла.
- §6. Волновые вектора связанных электронов кристалла.
- §7. Образование энергетических зон электронов в периодическом поле кристалла.
- §8. Инверсионная симметрия энергетических зон и приведенная зона Бриллюэна.
- §9. Металлы, диэлектрики и полупроводники с точки зрения зонной теории твердых тел.
- §10. Эффективная масса электронов в кристаллах.
- §11. О состояниях между эффективными массами связанных и свободных электронов кристалла.
- §12. Собственные полупроводники, понятие о дырках.
- §13. Примесно — дефектные состояния в полупроводниках.
- §14. Элементарная теория мелких примесных состояний полупроводника.
- §15. Зонная структура полупроводника в k пространстве.
В квантовой механике, как известно трансляционное движение электронов в кристалле под действием внешнего электрического поля можно описывать как распространение волнового пакета со скоростью:
Под действием силы внешнего электрического поля всякий электрон кристалла должен двигаться ускоренно:
Т.к. зависимость ![]() анизотропная, т.е. не одинакова в разных направлениях зоны Бриллюэна, то величины
анизотропная, т.е. не одинакова в разных направлениях зоны Бриллюэна, то величины ![]() в общем случае различны их значения образуют компоненты тензора II-го ранга:
в общем случае различны их значения образуют компоненты тензора II-го ранга:
Из (4) видно, что ![]() имеют размерность массы, а сами уравнения (4) выражают собой второй закон Ньютона для электронов кристалла под действием силы внешнего электрического поля. Из (4) следует, что под действием силы внешнего электрического поля электрон в периодическом поле кристалла, движется как двигался бы свободный электрон под действием этой силы если бы он имел массу (3). Величины
имеют размерность массы, а сами уравнения (4) выражают собой второй закон Ньютона для электронов кристалла под действием силы внешнего электрического поля. Из (4) следует, что под действием силы внешнего электрического поля электрон в периодическом поле кристалла, движется как двигался бы свободный электрон под действием этой силы если бы он имел массу (3). Величины ![]() являются компонентами тензора эффективной массы электронов в периодическом поле кристалла. С ее введением можно считать, что связанный электрон, под действием внешнего электрического поля, движется как свободный электрон, т.е. электрон не чувствует периодического поля кристаллической решетки и его движение можно описывать теми же законами, как и движение свободного электрона перемещающегося в анизотропной среде.
являются компонентами тензора эффективной массы электронов в периодическом поле кристалла. С ее введением можно считать, что связанный электрон, под действием внешнего электрического поля, движется как свободный электрон, т.е. электрон не чувствует периодического поля кристаллической решетки и его движение можно описывать теми же законами, как и движение свободного электрона перемещающегося в анизотропной среде.
Найдем эффективную массу свободного электрона, для которого закон дисперсии следующий:
Обычно записывают тензор обратной эффективной массы:
Так как вторая производная не зависит от порядка дифференцирования, то симметричный тензор II–го ранга обладает следующим свойством: оси координат в ![]() пространстве можно выбрать так, что все внедиагональные элементы будут равными нулю. Такие оси получили название главных осей координат. Впредь будем считать, что эффективная масса приведена к главным осям координат, тогда тензор обратной эффективной массы будет иметь вид:
пространстве можно выбрать так, что все внедиагональные элементы будут равными нулю. Такие оси получили название главных осей координат. Впредь будем считать, что эффективная масса приведена к главным осям координат, тогда тензор обратной эффективной массы будет иметь вид:
В общем случае характеризуется тремя компланарными отличными от нуля векторами, где ![]() главные оси координат.
главные оси координат.