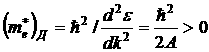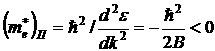Физика полупроводников. Лекция 2
- Физика полупроводников. Лекция 2
- §2. Адиабатическое приближение в квантовой теории твердых тел.
- §3. Одноэлектронное приближение в квантовой теории твердых тел.
- §4. Квантовая теория свободных электронов кристалла.
- §5. Волновая функция связанных электронов кристалла.
- §6. Волновые вектора связанных электронов кристалла.
- §7. Образование энергетических зон электронов в периодическом поле кристалла.
- §8. Инверсионная симметрия энергетических зон и приведенная зона Бриллюэна.
- §9. Металлы, диэлектрики и полупроводники с точки зрения зонной теории твердых тел.
- §10. Эффективная масса электронов в кристаллах.
- §11. О состояниях между эффективными массами связанных и свободных электронов кристалла.
- §12. Собственные полупроводники, понятие о дырках.
- §13. Примесно — дефектные состояния в полупроводниках.
- §14. Элементарная теория мелких примесных состояний полупроводника.
- §15. Зонная структура полупроводника в k пространстве.
Для примера качественно оценим эффективные массы в кристаллах Na. Электронами заполнены зоны 1s, 2s, 2p, 3s.
Произведем оценку эффективных масс для 1s и 3s. Скорость трансляционного движения электронов к каждой из зон равна:
![]() , скорость электронов в 3s зоне
, скорость электронов в 3s зоне ![]() , тогда из (5) следует, что эффективная масса электронов равна
, тогда из (5) следует, что эффективная масса электронов равна ![]() ; скорость электронов в 1s зоне
; скорость электронов в 1s зоне ![]() ,
, ![]() .
.
Из (1) видно, что скорость электронов под действием электрического поля тем больше, чем больше ширина зоны, а из (5) следует, что эффективная масса тем меньше, чем больше скорость, т.е. чем больше ширина зоны. Эффективная масса в широких зонах будет меньше.
Энергия внешнего электрического поля приложенного к кристаллу расходуется на изменение энергии электронов кристалла. При этом изменяется как кинетическая, так и потенциальная энергия электронов в кристалле. Полная энергия электрона сложным образом зависит от вектора ![]() и в разных кристаллах по разному
и в разных кристаллах по разному ![]() , и следовательно эффективная масса электронов в каждой зоне зависит от волнового вектора
, и следовательно эффективная масса электронов в каждой зоне зависит от волнового вектора ![]() , только в окрестности экстремальных точек каждой зоны эффективные массы не зависят от вектора
, только в окрестности экстремальных точек каждой зоны эффективные массы не зависят от вектора ![]() . Экстремальными называют те точки зоны Бриллюэна, которые соответствуют
. Экстремальными называют те точки зоны Бриллюэна, которые соответствуют ![]() и
и ![]() .
.
Действительно, в окрестности экстремальных точек, ![]() выражается параболической зависимостью, т.е.
выражается параболической зависимостью, т.е. ![]() . Для этого разложим
. Для этого разложим ![]() в ряд Тейлора в окрестности экстремальных точек и ограничимся первыми тремя членами разложения. Первая производная равна:
в ряд Тейлора в окрестности экстремальных точек и ограничимся первыми тремя членами разложения. Первая производная равна: 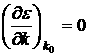 . Тогда зависимость
. Тогда зависимость ![]() вблизи дна зоны проводимости будет иметь вид:
вблизи дна зоны проводимости будет иметь вид: ![]() , A > 0.
, A > 0.
Зависимость ![]() вблизи потолка валентной зоны будет иметь вид:
вблизи потолка валентной зоны будет иметь вид:
Здесь ![]() отсчитывается от тех точек зоны Бриллюэна, где имеются
отсчитывается от тех точек зоны Бриллюэна, где имеются ![]() ,
, ![]() . Тогда эффективная масса электронов в окрестности
. Тогда эффективная масса электронов в окрестности ![]() будет равна:
будет равна:
Эффективная масса электронов в окрестности ![]() будет равна:
будет равна:
Кроме того, эффективная масса может быть как больше, так и меньше или же равна массе свободного электрона. Физическая причина такого поведения эффективной массы заключается в том, что под действием электрического поля меняется как кинетическая, так и потенциальная энергия электронов кристалла.
Будем обозначать через ![]() полную, кинетическую и потенциальную энергию электрона до приложения электрического поля, а через
полную, кинетическую и потенциальную энергию электрона до приложения электрического поля, а через ![]() соответственно после приложения электрического поля. Через
соответственно после приложения электрического поля. Через ![]() будем обозначать энергию внешнего электрического поля, передаваемого электронам кристалла. Для свободного электрона энергия
будем обозначать энергию внешнего электрического поля, передаваемого электронам кристалла. Для свободного электрона энергия ![]() идет только на изменение кинетической энергии: в отсутствии
идет только на изменение кинетической энергии: в отсутствии ![]() , после
, после ![]() . В кристаллах под действием электрического поля, движение связанных электронов меняется так, что энергия
. В кристаллах под действием электрического поля, движение связанных электронов меняется так, что энергия ![]() может затрачиваться как на изменение кинетической, так и потенциальной энергий.
может затрачиваться как на изменение кинетической, так и потенциальной энергий.
Рассмотрим четыре случая, которые могут иметь место в кристалле:
1) Под действием внешнего электрического поля кинетическая энергия увеличивается не только за счет энергии ![]() , но и за счет перехода части потенциальной энергии в кинетическую, тогда полная энергия электрона будет равна:
, но и за счет перехода части потенциальной энергии в кинетическую, тогда полная энергия электрона будет равна:
Отсюда следует, что изменение скорости связанного электрона под действием электрического поля будет больше чем для свободного электрона. Запишем второй закон Ньютона для свободных и связанных электронов, на которые действует одна и та же сила F: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() 2) В кристалле под действием электрического поля может реализоваться следующий случай, что часть энергии внешнего электрического поля
2) В кристалле под действием электрического поля может реализоваться следующий случай, что часть энергии внешнего электрического поля ![]() будет затрачиваться на увеличение потенциальной энергии электрона:
будет затрачиваться на увеличение потенциальной энергии электрона:
В этом случае изменение скорости движения связанного электрона под действием внешнего электрического поля будет меньшим, чем для свободного электрона, тогда: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
3) В некоторых кристаллах может реализовываться такой случай, что в присутствии внешнего электрического поля, потенциальная энергия кристалла увеличивается не только за счет энергии ![]() но и за счет перехода части кинетической энергии в потенциальную:
но и за счет перехода части кинетической энергии в потенциальную:
Из этого соотношения следует, что под действием электрического поля скорость электронов уменьшается, тогда: ![]() ,
, ![]() ,
, ![]() .
.
4) В кристалле может реализоваться и такой случай, что энергия внешнего электрического поля идет только на изменение кинетической энергии, а потенциальная энергия в поле не меняется, тогда:
Эффективная масса электронов в общем случае зависит от вектора ![]() зоны Бриллюэна, только в экстремальных точках эффективная масса постоянна, т.е. не зависят от
зоны Бриллюэна, только в экстремальных точках эффективная масса постоянна, т.е. не зависят от ![]() , это очень важно потому, что в частности состояние вблизи дна зоны проводимости и потолка валентной зоны определяет большинство физических свойств полупроводника.
, это очень важно потому, что в частности состояние вблизи дна зоны проводимости и потолка валентной зоны определяет большинство физических свойств полупроводника.