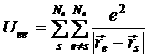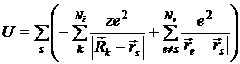Физика полупроводников. Лекция 2
- Физика полупроводников. Лекция 2
- §2. Адиабатическое приближение в квантовой теории твердых тел.
- §3. Одноэлектронное приближение в квантовой теории твердых тел.
- §4. Квантовая теория свободных электронов кристалла.
- §5. Волновая функция связанных электронов кристалла.
- §6. Волновые вектора связанных электронов кристалла.
- §7. Образование энергетических зон электронов в периодическом поле кристалла.
- §8. Инверсионная симметрия энергетических зон и приведенная зона Бриллюэна.
- §9. Металлы, диэлектрики и полупроводники с точки зрения зонной теории твердых тел.
- §10. Эффективная масса электронов в кристаллах.
- §11. О состояниях между эффективными массами связанных и свободных электронов кристалла.
- §12. Собственные полупроводники, понятие о дырках.
- §13. Примесно — дефектные состояния в полупроводниках.
- §14. Элементарная теория мелких примесных состояний полупроводника.
- §15. Зонная структура полупроводника в k пространстве.
 Одноэлектронное приближение определяет характер взаимодействия электронов кристалла друг с другом, т.е.
Одноэлектронное приближение определяет характер взаимодействия электронов кристалла друг с другом, т.е. ![]() . В этом приближении считается, что каждый электрон кристалла движется в кулоновских полях не только ядер, но и всех остальных электронов, кроме рассматриваемого. При этом это поле, как и в предыдущем случае, рассматривается как внешнее поле, независящее от мгновенного положения рассматриваемого электрона. В этом приближении потенциальная функция равна:
. В этом приближении считается, что каждый электрон кристалла движется в кулоновских полях не только ядер, но и всех остальных электронов, кроме рассматриваемого. При этом это поле, как и в предыдущем случае, рассматривается как внешнее поле, независящее от мгновенного положения рассматриваемого электрона. В этом приближении потенциальная функция равна:
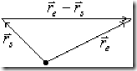
где 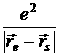 — потенциальная энергия s — электрона в кулоновском роле e — электрона,
— потенциальная энергия s — электрона в кулоновском роле e — электрона, 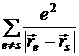 — потенциальная энергия s — электрона в поле всех остальных электронов кристалла,
— потенциальная энергия s — электрона в поле всех остальных электронов кристалла, 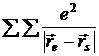 — потенциальная энергия всех электронов в кулоновском поле электронов кристалла.
— потенциальная энергия всех электронов в кулоновском поле электронов кристалла.
Значит в адиабатическом и одноэлектронном приближении потенциальная функция принимает вид:
В этих приближениях каждый электрон кристалла рассматривается как независимые друг от друга системы, значит, если мы имеем волновую функцию ![]() электронов кристалла, то ее можно представить в виде произведения одноэлектронных волновых функций:
электронов кристалла, то ее можно представить в виде произведения одноэлектронных волновых функций: ![]() , а их энергию в виде суммы энергий отдельных электронов:
, а их энергию в виде суммы энергий отдельных электронов:
В этих приближениях стационарное уравнение Шредингера для системы электронов кристалла распадается на Ne одноэлектронных стационарных уравнений Шредингера типа:
где ![]() и
и ![]() — это энергия s — электрона кристалла.
— это энергия s — электрона кристалла.
Теперь перейдем от ![]() координаты к текущей координате
координаты к текущей координате ![]() электрона, тогда уравнение (8) примет вид:
электрона, тогда уравнение (8) примет вид:
где ![]() — координаты рассматриваемого электрона,
— координаты рассматриваемого электрона, ![]() — его энергия,
— его энергия, ![]() — волновая функция электрона с координатой
— волновая функция электрона с координатой ![]() .
.
В адиабатическом приближении считается, что тепловое движение атомов кристалла сказывается на заполнении электронами их квантовых состояний, но не на самих состояниях.