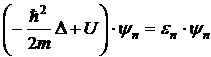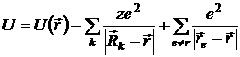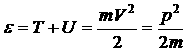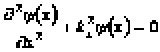Лекции для студентов

В адиабатическом и одноэлектронном приближениях состояние электронов кристалла описывается с помощью уравнения Шредингера:

(1)

.

Однако решение уравнения (1) представляет собой сложную задачу, потому что волновая функция электрона с координатой r () зависит от волновых функций всех остальных электронов через r_l, поэтому в квантовой теории твердых тел используются новые приближения. В частности всю совокупность электронов кристалла делят на три группы, в зависимости от степени их ионизации в объеме кристалла: свободные электроны, слабосвязанные электроны, сильно связанные электроны.

Свободные электроны — это электроны проводимости металла они “чувствуют” поле кристаллической решетки. Этот случай реализуется тогда, когда кинетическая энергия электрона больше абсолютной величины потенциальной энергии кристалла. Естественно на свободный электрон не действует сила электрического поля кристалла. В этом случае электрическое поле всех ядер скомпенсировано электрическим полем всех электронов кроме рассматриваемого: , следовательно, для свободного электрона .

Для свободных электронов кристалла существует потенциальный барьер лишь на его границе, обозначим через U₀ высоту потенциального барьера, для свободного электрона с нулевой энергией. Таким образом, в реальном кристалле свободный электрон движется в потенциальном ящике с “гладким” дном.

Рассмотрим 2 случая: 1) движение электрона в кристалле не ограниченных размеров и 2) в реальном кристалле.

1) Свободный электрон, движущийся в кристалле не ограниченных размеров не “чувствуют” не только периодического поля кристаллической решетки, но и не “чувствуют” границы. Как известно потенциальная энергия определяется с точностью до постоянной величины, поэтому потенциальную энергию электронов в кристалле можно принять равной , тогда полная энергия электрона равна:

.

Свяжем с направлением движения свободного электрона ось x и введем обозначения: , следовательно , видно что k_x имеет размерность обратной длине, т.е. она лежит в обратном пространстве.

,  — получил название волнового вектора. Стационарное уравнение Шредингера для свободного электрона вне ограниченном пространстве имеет вид:

(2)

,

. (3)

Решения уравнения (2) имеет вид:

(4)

Видно, что решением является совокупность двух бегущих волн, распространяющихся в противоположных направлениях. Представим себе, что электрон движется в положительном направлении оси x, тогда можно положить B = 0. Следовательно, амплитудная часть волновой функции свободного электрона, движущегося в неограниченном пространстве кристалла, в положительном направлении x имеет вид:

(5)

Полная волновая функция такого электрона в стационарном состоянии рана:

(6)

Если движение электрона не совпадает ни с одной осью координат и его положение характеризуется радиус-вектором , то полная волновая функция этого же электрона имеет вид:

(7)

Значения волнового вектора для свободного электрона движущегося в неограниченном пространстве, ничем не ограничено, принимает любые значения, следовательно, и энергия свободного электрона может принимать любые значения, т.е. энергия такого электрона не квантуется ее спектр сплошной.

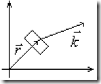
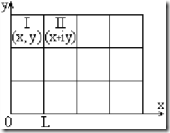
Если радиус-вектор характеризует место положения электронов в кристалле, то характеризует направление движения электрона, т.е. направление распространения электронной волны. Вектор перпендикулярен волновой поверхности одинаковой фазы. Теперь рассмотрим движение электрона в реальном кристалле, на границе реального кристалла существует потенциальный барьер, удерживающий свободные электроны внутри кристалла. Мысленно выделим внутри бесконечного кристалла некоторую область, которую разобьем на кубики с одинаковыми ребрами длиной L.

Точки I и II физически эквивалентные, тогда волновая функция электрона должна удовлетворять неравенству:

(8)

Из соотношения (8) следует, что , следовательно:

, ; , ; ,

, , .

Видно, что компоненты волнового вектора для электрона движущегося в ограниченной области кристалла квантуется, здесь L реальные размеры кристалла.

(9)

где . Из (9) видно, что энергия свободного электрона движущегося в кристалле ограниченного размера квантуется, следовательно, энергетический спектр такого электрона дискретный. Расстояние между двумя соседними энергетическими соседними уровнями .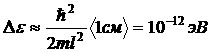

Видно, что очень малая величина, поэтому энергетический спектр свободного электрона в реальном кристалле называют квазинепрерывным. Разрывы не обнаруживаются экспериментом.