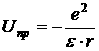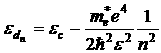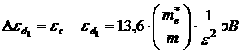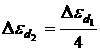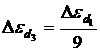Лекции для студентов

Как известно, мелкие примесные состояния такие, у которых энергия ионизации значительно меньше ширины запрещенной зоны .

Для определенности будем рассматривать полупроводник с мелкой донорной примесью, все выводы полученные для него будут верны для полупроводника с мелкой акцепторной примесью. Как известно орбита валентного электрона мелкого донора охватывает несколько постоянных решеток кристалла. В этом случае можно считать, что положительный ион донора взаимодействующий с валентным электроном погружен в диэлектрическую среду кристалла полупроводника. Тогда взаимодействие валентного электрона и иона можно считать по законам кулоновского взаимодействия точечных центров, следовательно, потенциальная энергия взаимодействия валентного электрона с положительным ионом будет равна:

 — диэлектрическая проницаемость кристалла. Тогда полная потенциальная энергия мелкого донора будет равна:

(1)

Запишем стационарное уравнение Шредингера для валентного электрона мелкого донора:

(2)

Запишем (2) в приближении эффективной массы, влияние периодического поля кристалла учтем заменой

(3)

(3) совпадает с уравнением атома водорода, если заменить , 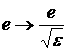. Значит, решение уравнения (3) такое же, как для атома H, только при соответствующих заменах.

, (4)

Из (4) следует, что энергия мелкого донора квантуется, состояние с  — это основное состояние и ему соответствует энергия:

(5)

Тогда энергия ионизации в основном состоянии равна:

(6)

Из (6) следует, что энергия ионизации мелких доноров не зависит от их сорта, т.е. что энергия ионизации одинакова для любой мелкой примеси в данном кристалле. Энергия ионизации возбужденного состояния мелкого донора рвана:

, , , то .

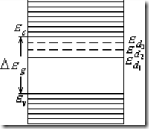
На рисунке показана энергетическая диаграмма кристалла с донорной примесью. Для того чтобы экспериментально обнаружить состояние мелких доноров нужно использовать низкие температуры и технику миллиметрового диапазона.