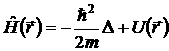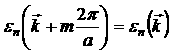Физика полупроводников. Лекция 2
- Физика полупроводников. Лекция 2
- §2. Адиабатическое приближение в квантовой теории твердых тел.
- §3. Одноэлектронное приближение в квантовой теории твердых тел.
- §4. Квантовая теория свободных электронов кристалла.
- §5. Волновая функция связанных электронов кристалла.
- §6. Волновые вектора связанных электронов кристалла.
- §7. Образование энергетических зон электронов в периодическом поле кристалла.
- §8. Инверсионная симметрия энергетических зон и приведенная зона Бриллюэна.
- §9. Металлы, диэлектрики и полупроводники с точки зрения зонной теории твердых тел.
- §10. Эффективная масса электронов в кристаллах.
- §11. О состояниях между эффективными массами связанных и свободных электронов кристалла.
- §12. Собственные полупроводники, понятие о дырках.
- §13. Примесно — дефектные состояния в полупроводниках.
- §14. Элементарная теория мелких примесных состояний полупроводника.
- §15. Зонная структура полупроводника в k пространстве.
Кривые зависимости ![]() для различных энергетических зон отличаются друг от друга, но энергия в каждой зоне n является четной функцией волнового вектора
для различных энергетических зон отличаются друг от друга, но энергия в каждой зоне n является четной функцией волнового вектора ![]() , т.е.
, т.е. ![]() . Действительно, рассмотрим одноэлектронное уравнение Шредингера для связанного электрона в кристалле.
. Действительно, рассмотрим одноэлектронное уравнение Шредингера для связанного электрона в кристалле.
Наряду с уравнением (1) рассмотрим комплексно сопряженное уравнение Шредингера:
Так как ![]() и
и ![]() является вещественными, то знаки комплексного сопряжения можно опустить, тогда (2) принимает вид:
является вещественными, то знаки комплексного сопряжения можно опустить, тогда (2) принимает вид:
Функция ![]() входящая в (3) является Блоховской, потому что ей соответствует оператор
входящая в (3) является Блоховской, потому что ей соответствует оператор ![]() , инвариантный относительно трансляции на собственные вектора
, инвариантный относительно трансляции на собственные вектора ![]()
Значит, Блоховской функции ![]() соответствует волновой вектор
соответствует волновой вектор ![]() . Сравнивая уравнения (1) и (3) приходим к выводу, что
. Сравнивая уравнения (1) и (3) приходим к выводу, что ![]() , т.е. энергия в каждой n зоне является четной функцией волнового вектора или иными словами, каждая энергетическая зона кристалла обладает инверсионной симметрией относительно точки Г, центра первой зоны Бриллюэна.
, т.е. энергия в каждой n зоне является четной функцией волнового вектора или иными словами, каждая энергетическая зона кристалла обладает инверсионной симметрией относительно точки Г, центра первой зоны Бриллюэна. ![]() .
.
Следовательно, приведенный на рисунке §7 энергетический спектр электронов кристалла обладает зеркальной симметрией относительно оси ординат. Нами показано в §6, что энергия электронов в каждой зоне является периодической функцией с периодом обратной решетки:
Для одномерного кристалла период обратной решетки равен ![]() . При этом обратная решетка является одномерной
. При этом обратная решетка является одномерной
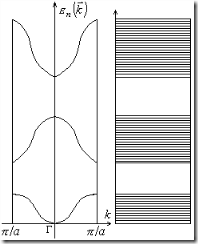 Пунктирными линиями на рисунке §7 отражен факт периодичности энергий в обратном пространстве решетки. В связи с периодичностью функции
Пунктирными линиями на рисунке §7 отражен факт периодичности энергий в обратном пространстве решетки. В связи с периодичностью функции ![]() , соотношение (5), нет необходимости изображать все зоны Бриллюэна, а можно использовать только первую зону Бриллюэна, в которой приведены кривые
, соотношение (5), нет необходимости изображать все зоны Бриллюэна, а можно использовать только первую зону Бриллюэна, в которой приведены кривые ![]() ,
, ![]() … В этом случае первая зона Бриллюэна получает название приведенной зоны Бриллюэна. Используя приведенную зону Бриллюэна можно получить всю энергетику кристалла. В этом случае энергетический спектр кристалла будет качественно выглядеть так, как показано на рисунке.
… В этом случае первая зона Бриллюэна получает название приведенной зоны Бриллюэна. Используя приведенную зону Бриллюэна можно получить всю энергетику кристалла. В этом случае энергетический спектр кристалла будет качественно выглядеть так, как показано на рисунке.