Лекции для студентов

Слабосвязанные электроны кристалла соответствуют состоянию валентных электронов кристалла. Они занимают значительную часть объема кристалла, поэтому волновые функции соседних электронов сильно перекрываются.

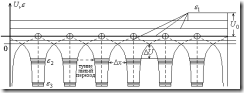Сильно связанным электронам соответствует те электроны, которые расположены близко к ядру атома, для них характерны большие значения сил взаимодействия с ядром. Т.е. для этих электронов потенциальная функция сильно изменяется с изменением . Сильно связанные электроны занимают не значительную часть кристалла. Связанные электроны кристалла находятся в потенциальных ямах, образованных в результате перекрытия потенциальных барьеров соседних атомов кристалла.

 — ширина барьера, сквозь которого происходит туннелирование,  — высота потенциального барьера. Штрих пунктирной линией обозначены потенциальные функции изолированных атомов кристалла. Сплошными линиями обозначен потенциальный рельеф атома кристалла, полученных в результате перекрытия потенциальных барьеров соседних атомов. Энергия , которая выше значения “потолка” потенциальных барьеров соответствует энергии свободных электронов . Энергии и соответствуют энергии связанных электронов, естественно энергия слабо связанных электронов (валентных) выше энергии сильно связанных электронов .  — энергия, которую нужно сообщить электрону (самому холодному), чтобы “вырвать” его из кристалла.

Связанные электроны в кристаллах могут перемещаться от одного атома к другому, в отличие от изолированных атомов такой переход осуществляется туннельным способом (без потери энергии). Такой переход будет тем более вероятен, чем меньше его высота. Поэтому связанные электроны, как и свободные не принадлежат отдельному атому, т.е. принадлежат всему кристаллу, они коллективизированы.

В результате того, что атомы твердого тела взаимодействуют между собой, их уровни расщепляются в зоны. Так как взаимодействие слабосвязанных электронов сильнее чем у сильно связанных, то их зона энергии будет шире, чем у сильно связанных.

Найдем вид волновой функции связанного электрона кристалла, для этого запишем стационарное уравнение Шредингера, для такого электрона:

(1)

(1΄)

Уравнение (1) и (1΄) относятся к электрону с координатой . Знак ΄ у второй означает, что суммирование происходит по всем электронам кроме электрона с координатой .

В 1928г. F. Bloch предположил, что плотность электрического заряда ядер и электронов в среднем одинакова по времени во всех элементарных ячейках кристалла. Поэтому электрическое поле создаваемое данной системой заряда кристалла должно быть периодическим с периодом кристаллической решетки, следовательно, и потенциальная энергия каждого связанного электрона кристалла должна быть периодической функцией с периодом кристаллической решетки кристалла.

(2)

.

(2) означает, что потенциальная энергия электронов одинакова в физически эквивалентных точках кристалла.

Введем оператор который, действуя на функцию координат переводит ее в , .

Подействуем на правую и левую часть уравнения (1) оператором , получим:

(3)

То есть, инвариантен относительно трансляции на собственные вектора.  — это компоненты вектора , числа. Тогда (3) можно записать:

(4)

Исходя из (3) и (4) можно сказать, что операторы , коммутируют между собой .

Из квантовой механики известно, что если коммутирует с оператором Гамильтона , то собственные функции (волновые функции) оператора одновременно являются собственными функциями оператора :

(5)

где  — число, вообще говоря, комплексное, являющиеся собственным значением оператора .

Найдем, как зависит от вектора , для этого сначала будем считать, что волновые функции связанных электронов кристалла нормированы на “1”. Т.е. будем считать, что квадрат модуля волновой функции равен вероятности нахождения электрона в точке с координатой .

, тогда  — вероятность нахождения электрона в элементе . При таком подходе интеграл по всему пространству, где находится электрон равен:

, , (6)

Подействуем на функцию последовательно операциями сдвига на вектор

Тогда , Значит

(7)

Из (7) следует, что зависит от экспоненциально, так как при умножении экспоненциальной функции их аргументы складываются, т.е.

(8)

где имеет размерность обратную длине (волновой вектор), это вещественный вектор, если бы он был комплексным, то он бы не удовлетворял соотношению (6).

Учитывая (8) равенство (5) приобретает вид:

(9)

(9) это единственное условие определяющее вектор . Из (9) следует, что

(10)

Покажем, что  — периодическая функция с периодом кристаллической решетки.

Значит, волновая функция стационарного состояния электрона кристалла имеет вид:

(12)

Из (12) видно, что волновая функция связанного электрона представляет собой бегущую волну, амплитуда которой промодулированна с периодом кристаллической решетки. Это функция получила название Блоховской функции.

Периодичность амплитуды Блоховской функции, является следствием периодичности потенциальной энергии связанных электронов. Из (12) следует, что вероятность обнаружения электрона одинакова во всех физически эквивалентных точках кристалла ( и физически эквивалентны):

Но эта вероятность не одинакова в различных точках элементарной ячейки кристалла, что является результатом неоднородности пространства в котором движется связанный электрон (в отличие от свободных электронов кристалла).