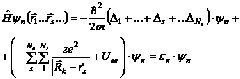Физика полупроводников. Лекция 2
- Физика полупроводников. Лекция 2
- §2. Адиабатическое приближение в квантовой теории твердых тел.
- §3. Одноэлектронное приближение в квантовой теории твердых тел.
- §4. Квантовая теория свободных электронов кристалла.
- §5. Волновая функция связанных электронов кристалла.
- §6. Волновые вектора связанных электронов кристалла.
- §7. Образование энергетических зон электронов в периодическом поле кристалла.
- §8. Инверсионная симметрия энергетических зон и приведенная зона Бриллюэна.
- §9. Металлы, диэлектрики и полупроводники с точки зрения зонной теории твердых тел.
- §10. Эффективная масса электронов в кристаллах.
- §11. О состояниях между эффективными массами связанных и свободных электронов кристалла.
- §12. Собственные полупроводники, понятие о дырках.
- §13. Примесно — дефектные состояния в полупроводниках.
- §14. Элементарная теория мелких примесных состояний полупроводника.
- §15. Зонная структура полупроводника в k пространстве.
Твердое тело представляет собой систему огромного числа взаимодействующих между собой заряженных частиц, ядер и электронов. Состояние твердого тела в квантовой механике можно описывать с помощью волновой функции ![]() , где
, где ![]() и
и ![]() — радиусы векторы s — электрона и k — ядра. Будем считать, что кристалл состоит из атомов одного типа с порядком Z, обозначим через Ni — число ядер кристалла, тогда число электронов кристалла
— радиусы векторы s — электрона и k — ядра. Будем считать, что кристалл состоит из атомов одного типа с порядком Z, обозначим через Ni — число ядер кристалла, тогда число электронов кристалла ![]() .
.
Волновую функцию кристалла можно представить в виде произведения:
![]() — амплитудная часть волновой функции кристалла, зависящая только от координат ядер и электронов. А стационарное состояние ∆ (оператор Гамильтона) не зависит от температуры, амплитудная часть волновой функции должна удовлетворять следующему уравнению Шредингера:
— амплитудная часть волновой функции кристалла, зависящая только от координат ядер и электронов. А стационарное состояние ∆ (оператор Гамильтона) не зависит от температуры, амплитудная часть волновой функции должна удовлетворять следующему уравнению Шредингера:
m, M — массы электрона и ядра соответственно. Где ![]() и
и ![]() — операторы Лапласа по координатам s электрона и k ядра,
— операторы Лапласа по координатам s электрона и k ядра, ![]() — полная энергия кристалла. U — потенциальная функция кристалла, она представляет собой сумму потенциальной энергии ядер и электронов кристалла во внешнем электрическом поле (Uвн), потенциальную энергию электронов в поле ядер (Uei), потенциальную энергию взаимодействия электронов друг с другом (Uee), потенциальную энергию взаимодействия ядер с ядрами (Uii):
— полная энергия кристалла. U — потенциальная функция кристалла, она представляет собой сумму потенциальной энергии ядер и электронов кристалла во внешнем электрическом поле (Uвн), потенциальную энергию электронов в поле ядер (Uei), потенциальную энергию взаимодействия электронов друг с другом (Uee), потенциальную энергию взаимодействия ядер с ядрами (Uii):
В стационарных условиях потенциальная функция не должна явно зависеть от времени, она зависит только от координат электронов ядер, тогда ![]() ,
, 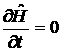
Для получения информации о состояниях кристалла необходимо в каждом конкретном случае знать явный вид функции U, после этого необходимо эту функцию подставить в уравнение Шредингера (2) и решить его относительно ![]() и
и ![]() . Однако такая задача математически сложная (практически не решаемая), из-за невозможности получить функцию U в явном виде. Кроме того, функция U зависит от состояния системы и изменяется с изменением последней. По этой причине в квантовой теории твердых тел используется ряд приближений. Они выбираются с таким расчетом, чтобы в задаче сохранились наиболее существенные черты системы и отбрасываются малосущественные свойства. В частности в зонной теории твердых тел используется адиабатическое приближение и одноэлектронное приближение.
. Однако такая задача математически сложная (практически не решаемая), из-за невозможности получить функцию U в явном виде. Кроме того, функция U зависит от состояния системы и изменяется с изменением последней. По этой причине в квантовой теории твердых тел используется ряд приближений. Они выбираются с таким расчетом, чтобы в задаче сохранились наиболее существенные черты системы и отбрасываются малосущественные свойства. В частности в зонной теории твердых тел используется адиабатическое приближение и одноэлектронное приближение.
Адиабатическим называется такой процесс, который протекает без обмена энергии с окружающей средой (быстро протекающие процессы). В адиабатическом приближении задача о движении электронов и ядер в твердом теле заменяется задачей о движении только электронов в заданной решетке из ядер. Ядра считаются неподвижными источниками кулоновского поля, действующего на электроны кристалла. При этом это поле рассматривается, как внешнее, т.е. оно зависит от мгновенного положения электронов. Такое адиабатическое приближение обосновано тем, что масса электронов значительно меньше массы ядер ![]() и поэтому, скорость движения электронов будет значительно больше скорости движения ядер
и поэтому, скорость движения электронов будет значительно больше скорости движения ядер ![]() .
. 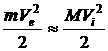 . Поэтому даже если ядра находятся вне равновесном состоянии, электроны всякий раз успевают прийти в равновесное состояние. Следовательно, а адиабатическом приближении волновая функция кристалла
. Поэтому даже если ядра находятся вне равновесном состоянии, электроны всякий раз успевают прийти в равновесное состояние. Следовательно, а адиабатическом приближении волновая функция кристалла ![]() , в уравнении (2) будет зависеть только от координат электронов.
, в уравнении (2) будет зависеть только от координат электронов.
Координаты ядер будут входить как параметры, таким образом, в адиабатическом приближении волновая функция представляет собой волновую функцию только электронов.
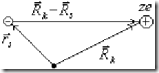 Будем считать, что внешнее электрическое поле выключено, т.е. Uвн = 0. Очевидно в адиабатическом приближении из потенциальной функции (3) можно исключить слагаемое Uii, тогда
Будем считать, что внешнее электрическое поле выключено, т.е. Uвн = 0. Очевидно в адиабатическом приближении из потенциальной функции (3) можно исключить слагаемое Uii, тогда
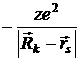 — это потенциальная энергия s — электрона в поле k — ядра. Тогда потенциальная энергия s — электрона в поле всех ядер будет равна:
— это потенциальная энергия s — электрона в поле k — ядра. Тогда потенциальная энергия s — электрона в поле всех ядер будет равна: 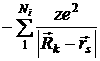 .
.
Потенциальная энергия электронов в поле всех ядер будет определяться двойной суммой: 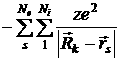 .
.
Запишем стационарное уравнение Шредингера кристалла в адиабатическом приближении:
![]() — полная энергия электронной системы кристалла.
— полная энергия электронной системы кристалла.