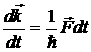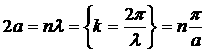Лекции для студентов

Для определенности рассмотрим кристалл в виде линейной цепочки периодически расположенных атомов (одномерный кристалл). Пусть a — период кристалла.

Обратная решетка такого кристалла будет также линейной (одномерной) с периодом равным .

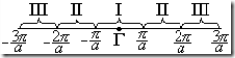Первая зона Бриллюэна занимает интервал от до , вторая зона Бриллюэна занимает интервал от до и от до , третья зона Бриллюэна занимает интервал от до и от до .

Рассмотрим с квантово-механической точки зрения трансляционное (направленное) движение связанного электрона такого одномерного кристалла под действием внешнего электрического поля , действующего вдоль цепочки атомов. Движение электрона под действием поля будем рассматривать не как движение микрочастицы, а как распространение электромагнитной волны вдоль цепочки атомов, в положительном направлении оси x, такую ситуацию можно создать в трех мерном кристалле, если приложить поле вдоль цепочки одинаковых атомов кристалла.

Связанный электрон кристалла, как коллективизированная частица локализован в достаточно большой области пространства: ∆x ~ L, тогда в соответствии с соотношением неопределенности ∆x∆p ~ ħ, неопределенность значения импульса связанного электрона и его энергии очень мала, потому что ∆x велико; следовательно в этом случае состояние связанных электронов можно описывать путем суперпозиции стоячих волн с близкими значениями волновых векторов; т.е. состояние связанного электрона мы можем описывать с помощью волнового пакета, движущегося со скоростью . С этой скоростью и перемещается электрон под действием электрического поля. Свободный электрон кристалла под действием электрического поля движется так, что его энергия в зависимости от волнового вектора изменяется по параболическому закону: .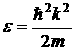

Выясним в общих чертах характер зависимости энергии связанных электронов от волнового вектора . Для упрощения подхода к решению этой задачи заменим реальный потенциальный рельеф цепочки атомов системой потенциальных прямоугольных ям, находящихся друг от друга на расстоянии a и разделенных пря

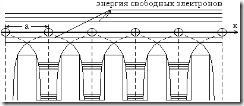моугольными потенциальными барьерами одинаковой толщины.

Пусть связанный электрон под действием внешнего электрического поля с силой начинает трансляционное движение из состояния характеризуемого, например и . Пусть электрическое поле направлено вдоль оси OX, как показано на рисунке. В данном случае связанные элементы движутся перпендикулярно стенкам потенциальных ям. На пути внешнее поле производит работу: , она затрачивается на изменение энергии электрона:

(1)

Скорость трансляционного движения электрона определяется скоростью движения волнового пакета:

(2)

Из (1) следует, что

(3)

Подставляя (3) в (2), получим:

(4)

Или в векторной форме:

(5)

Изменение волнового вектора совпадает с направлением силы . Из (1) и (2) следует, что со временем значение волнового вектора увеличивается. В соответствии с соотношением , увеличение значения вектора соответствует уменьшению длины электронной волны.

Электронная волна в кристалле частично отражается от всех стенок потенциальных барьеров, унося с собой часть энергии электрона. До тех пор пока не выполнится условие Вульфа — Брэггов: , .

Отраженные волны будут иметь различные фазы. Накладываясь друг на друга они будут гасить эти волны и следовательно, прямая волна будет распространяться по кристаллу почти не рассеиваясь. Т.е. связанный электрон, параметры которого удовлетворяет соотношению Вульфа — Брэггов, будет двигаться как свободный электрон. Его энергия зависит от волнового вектора параболично. В нашем случае электронная волна перпендикулярна стенкам потенциальных барьеров: . Следовательно, соотношение Вульфа — Брэггов для нашего случая имеет вид:

(6)

Из (6) следует, что волновой вектор лежит на границе зон Бриллюэна, n = 1 — на границе первой зоны Бриллюэна, n = 2 — на границе второй зоны Бриллюэна и т.д.

Когда со временем значение волнового вектора будет принадлежать и соотношению (6), то фазы отраженных электронных волн будут иметь близкие значение и следовательно, отраженные волны будут ослаблять прямую волну. Когда значение волнового вектора в точности удовлетворяет условию Вульфа — Брэггов (6) интенсивность отраженной электронной волны будет совпадать с интенсивностью прямой волны.

Кроме того, эти волны имеют одинаковую частоту и поляризацию, т.е. в кристалле образуются две бегущие волны, распространяющиеся в противоположных направлениях. В результате суперпозиции этих волн образуется стоячая волна. Значит, когда , электронные волны в кристалле — стоячие волны.

Из двух бегущих волн, как известно можно сформировать две стоячие волны, которые будут являться решением уравнения Шредингера для связанных электронов кристалла при :

(7)

(8)

Знак “+” означает, что функция  — четная относительно x, “-” означает, что функция  — нечетная относительно x.

Значит, в точке имеется два решения уравнения Шредингера, которому соответствует два разных значений энергий , т.е. в точке на границе зон Бриллюэна имеется скачок энергий. Величину скачка обозначим: .

Скачок энергии объясняется тем, что в этом случае имеются группировки элементов в разных по отношению к положительным ионам областям пространства. Функция дает пучности плотности электронного заряда в точках кристалла, соответствующих центрам положительных ионов, уменьшая тем самым их потенциальную энергию. Функция дает пучности плотности электронного заряда в точках кристалла по средине между соседними атомами.

Действительно плотность электронного заряда в точке или .  — плотности зарядов.

(9)

(10)

Положение центров ионов: , Положение точек на середине между соседними атомами: ,

Легко показать, что и имеют максимальное значение в точках: и соответственно. ,

Значит, состояниям связанного электрона, характеризуемые волновыми векторами от 0 до (пол первой зоны Бриллюэна), соответствует интервал разрешенных энергий , минимальное значение энергии в котором , а максимальное значение энергии обозначим . Состояниям электрона в интервале от до (пол второй зоны Бриллюэна) соответствует интервал разрешенных энергий , минимальное значение в котором , а максимальное значение . В точке имеет место скачок энергий равный . Энергию внутри интервала электрон не может иметь, это зона запрещенных энергий. Состояниям электрона в интервале от до (пол третьей зоны Бриллюэна) соответствует интервал разрешенных энергий , минимальное значение в котором , а максимальное значение , и т.д.

Совокупность разрешенных энергий: , , и т.д. образуют зоны разрешенных энергий кристалла (или разрешенные энергетические зоны). Промежутки энергий: образуют зоны запрещенных энергий кристалла (смотри рисунок). На этом рисунке показана качественная зависимость энергии электронов в периодическом поле одномерного кристалла.

Вблизи точки Г . Очевидно первую зону энергии будут занимать сильно связанные электроны, т.е. те которые будут непосредственно возле ядра атомов. Вторую зону занимают электроны, которые находятся дальше от ядра и т.д. Самая верхняя заполненная зона будет содержать валентные электроны. Валентные электроны “чувствуют” влияние соседних атомов кристалла, поэтому их зона будет более широкой.