Лекции для студентов

Как следует из (12) волновая функция связанных электронов кристалла зависит от волнового вектора , различным значениям вектора соответствует, вообще говоря, разные волновые функции. В теории твердых тел волновые вектора выступают в качестве квантовых чисел определяющих состояние электронов в периодическом поле кристалла. Запишем равенство, которое связывает волновые функции с вектором :

(1)

(1) единственное условие определяющее волновой вектор , но равенство (1) выполняется если вектор заменить на эквивалентный вектор

(2)

Значит, вектора определяющие состояния связанных электронов кристалла вводятся с точностью до свободных векторов обратной решетки, т.е. состояние связанных электронов, с волновыми векторами и физически не различны, следовательно все физические величины определяющие состояния электронов в периодическом поле кристалла периодичны с периодом обратной решетки:

, .

Совокупность не эквивалентных векторов, которые однозначно определяют состояние электронов в периодическом поле кристалла, образуют в обратном пространстве область, которая называется первой зоной Бриллюэна.

В первой зоне Бриллюэна содержится бесконечное число волновых векторов , но очевидно, что в кристаллах конечных размеров состояние связанных электронов должны характеризоваться конечным числом разрешенных волновых векторов, найдем это число.

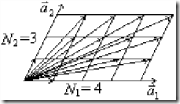
Конечные размеры реальных кристаллов нарушают его трансляционную симметрию относительно векторов . Для ее сохранения в кристаллах конечных размеров вводят так называемые граничные циклические условия Кармана — Борна. Представим себе, что реальный кристалл имеет форму параллелепипеда со сторонами , направленными вдоль базисных векторов (кристаллографических осей), N>>1. Представим к такому кристаллу бесконечное множество таких же кристаллов и получим кристалл бесконечных размеров, для которых сохраняется трансляционная симметрия (смотри рисунок).

Кристаллы ничем не выделены, они не “чувствуют” границы, очевидно при трансляции кристалла на вектора физические точки кристалла, например A, совмещаются с физически эквивалентными точками A₁, A₂ соседних кристаллов.

, , , .

Как известно первой зоне Бриллюэна принадлежат вектора удовлетворяющие неравенству , , , следовательно, принимает N значений.

Значит, проекции разрешенных векторов первой зоны Бриллюэна на любой базисный вектор имеет дискретный ряд значений и число этих значений равно N, отсюда следует, что число разрешенных значений волновых векторов однозначно характеризующих состояние связанных электронов кристалла конечных размеров равно N³, т.е. равно числу элементарных ячеек кристалла.

Разность значений двух соседних разрешенных волновых векторов очень мала в направлении для векторов параллельных базисным векторам, эта разность составляет . L — линейные размеры кристалла в направлении базисного вектора.

Действительно, , если , тогда ,

, , .

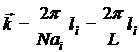
Поэтому дискретность волновых векторов не проявляется на опыте (зависимость какой-нибудь физической величины от волнового вектора называется спектром этой величины), следовательно, такие спектры являются практически непрерывными, квазинепрерывными.