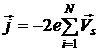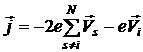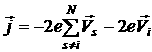Физика полупроводников. Лекция 2
- Физика полупроводников. Лекция 2
- §2. Адиабатическое приближение в квантовой теории твердых тел.
- §3. Одноэлектронное приближение в квантовой теории твердых тел.
- §4. Квантовая теория свободных электронов кристалла.
- §5. Волновая функция связанных электронов кристалла.
- §6. Волновые вектора связанных электронов кристалла.
- §7. Образование энергетических зон электронов в периодическом поле кристалла.
- §8. Инверсионная симметрия энергетических зон и приведенная зона Бриллюэна.
- §9. Металлы, диэлектрики и полупроводники с точки зрения зонной теории твердых тел.
- §10. Эффективная масса электронов в кристаллах.
- §11. О состояниях между эффективными массами связанных и свободных электронов кристалла.
- §12. Собственные полупроводники, понятие о дырках.
- §13. Примесно — дефектные состояния в полупроводниках.
- §14. Элементарная теория мелких примесных состояний полупроводника.
- §15. Зонная структура полупроводника в k пространстве.
Химически чистые (беспримесные и бездефектные) полупроводники называются собственными. Собственными дефектами полупроводника являются вакансии, междоузельные атомы и т.д. Свойства собственных полупроводников определяются в основном характеристиками и параметрами валентной зоны и зоны проводимости, шириной запрещенной зоны, эффективной массы электронов и дырок, плотностью постоянной вблизи краев зон (число разрешенных состояний приходящиеся на единичный интервал энергии) и т.д. При T = 0 K0 полупроводники не проводят ток, при нагревании некоторые электроны валентной зоны получают достаточную энергию для их перехода в зону проводимости. Под действием других внешних факторов (освещение, облучение и т.д.) электроны перешедшие в зону проводимости могут участвовать в переносе электрического тока, кроме того, вакантные уровни в валентной зоне также могут участвовать в переносе тока за счет переходов других электронов этой зоны на вакантные уровни. В отсутствии электрического поля такие переходы равновероятны во всех направлениях кристалла. При приложении электрического поля наблюдается преимущественное перемещение электронов в зоне проводимости и валентной зоне в направлении против электрического поля.
Рассмотрим более подробно вопрос об участии электронов валентной зоны в переносе электрического тока. Под действием электрического поля любой электрон кристалла создает мгновенный ток плотностью ![]() . Действительно, мысленно выделим в кристалле параллелепипед с ребром длиной
. Действительно, мысленно выделим в кристалле параллелепипед с ребром длиной ![]() и площадью поперечного сечения
и площадью поперечного сечения ![]() .
. ![]() — скорость электрона направленного движения в электрическом поле,
— скорость электрона направленного движения в электрическом поле, ![]() — число электронов в единице объема кристалла.
— число электронов в единице объема кристалла. ![]() — путь проходимый электроном за время
— путь проходимый электроном за время ![]() .
. ![]() — число электронов в выделенном объеме. За время
— число электронов в выделенном объеме. За время ![]() все электроны, находящиеся в объеме параллелепипеда пересекут площадку
все электроны, находящиеся в объеме параллелепипеда пересекут площадку ![]() и перенесут заряд
и перенесут заряд ![]() :
: ![]() . Плотность тока переносимого этим зарядом:
. Плотность тока переносимого этим зарядом: ![]() . Плотность тока переносимого одним электроном равна:
. Плотность тока переносимого одним электроном равна: ![]() .
.
Рассмотрим два случая:
1) Пусть валентная зона полностью заполнена электронами. Состояние электронов в кристалле, как известно, можно характеризовать волновыми векторами из первой зоны Бриллюэна. В частности скорость движения электронов в электрическом поле характеризуется, например волновыми векторами ![]() . Будем обозначать скорость
. Будем обозначать скорость ![]() , тогда результирующая плотность тока связанная с движением всех валентных электронов кристалла будет равна:
, тогда результирующая плотность тока связанная с движением всех валентных электронов кристалла будет равна:
Множитель 2 появился из-за принципа Паули: на каждом уровне может находиться только 2 электрона с противоположными спинами. ![]() — скорость волнового пакета.
— скорость волнового пакета.
Скорость электронов в каждой зоне является нечетной функцией волнового вектора. Нам известно, что зона Бриллюэна симметрична относительно вектора ![]() , т.е. для каждого вектора
, т.е. для каждого вектора ![]() есть обратный ему вектор
есть обратный ему вектор ![]() , тогда
, тогда ![]() . Следовательно, согласно соотношению (1)
. Следовательно, согласно соотношению (1) ![]() . Это означает, что полностью заполненная электронами валентная зона не может проводить ток.
. Это означает, что полностью заполненная электронами валентная зона не может проводить ток.
2) Представим себе, что под воздействием внешнего фактора один валентный электрон, характеризуемый волновым вектором ![]() , перешел из валентной зоны в зону проводимости, но один электрон характеризуемый
, перешел из валентной зоны в зону проводимости, но один электрон характеризуемый ![]() остался. В соответствии с соотношением (1) плотность тока, обеспечиваемая всеми валентным электронами кроме одного, будет равной.
остался. В соответствии с соотношением (1) плотность тока, обеспечиваемая всеми валентным электронами кроме одного, будет равной.
Второе слагаемое справа — это оставшийся без пары электрон в зоне ![]() . Если бы один валентный электрон не перешел бы в зону проводимости, то равенство (1) для полностью заполненной зоны будет:
. Если бы один валентный электрон не перешел бы в зону проводимости, то равенство (1) для полностью заполненной зоны будет:
Равенство (2) можно записать:
 Из (3) следует, что суммарный ток, связанный с движением электронов валентной зоны, в которой один электрон перешел в зону проводимости, эквивалентен току переносимому частицей с положительным зарядом
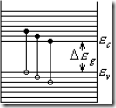
Из (3) следует, что суммарный ток, связанный с движением электронов валентной зоны, в которой один электрон перешел в зону проводимости, эквивалентен току переносимому частицей с положительным зарядом ![]() , который занимает состояние электрона перешедшего в зону проводимости. Такая фиктивная частица с положительным зарядом, численно равная заряду электрона получила название дырки. Придание дырке положительного заряда потребовало придать электронам, соответствующим потолку валентной зоны, положительного значения эффективной массы. Действительно в переходах: валентная зона — зона проводимости, участвуют электроны валентной зоны, расположенные вблизи ее дна (смотри рисунок).
, который занимает состояние электрона перешедшего в зону проводимости. Такая фиктивная частица с положительным зарядом, численно равная заряду электрона получила название дырки. Придание дырке положительного заряда потребовало придать электронам, соответствующим потолку валентной зоны, положительного значения эффективной массы. Действительно в переходах: валентная зона — зона проводимости, участвуют электроны валентной зоны, расположенные вблизи ее дна (смотри рисунок).
При всех тепловых и иных межзонных переходах электроны заполняют состояние вблизи дна зоны проводимости и дырки вблизи потолка валентной зоны. Как известно, состояние вблизи потолка валентной зоны характеризуется отрицательной эффективной массой, но состояние вблизи потока валентной зоны это состояние дырок, имеющих положительный заряд, тогда запишем второй закон Ньютона для электронов и дырок соответственно:
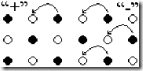
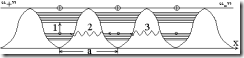
Движение дырок под действием внешнего электрического поля можно пояснить при помощи следующего рисунка.
На следующем рисунке показана схема трансляционного движения дырки в условиях потенциального рельефа кристаллической решетки.
1 — тепловой переход электрона из валентной в зону проводимости и образование дырки в валентной зоне, 2, 3, 4… — туннельные переходы валентных электронов атомов кристалла в незаполненные состояния валентной зоны, приводящие к движению дырки вправо.
 |
Как уже подчеркивалось, реальными переносчиками электрического тока в валентной зоне и зоне проводимости являются электроны, а не формально введенные частицы дырки. Введение понятие дырок оказалось плодотворным в физике полупроводников. Дело в том, что классические законы применимы к частицам с небольшой концентрацией. Концентрация электронов в зоне проводимости