Лекции для студентов

Лекция по “Теории полёта”. Часть 1

  Силы и моменты действующие на ракету в полете

Аэродинамические силы

             Все аэродинамические силы , действующие на ракету в полете можно свести к одной результирующей силе  R_A , а также к результирующему моменту , действующему относительно масс ракеты .

             R_A проходит через точку на продольной оси ракеты , которая носит название центр давления ракеты .

             Величина и направление R_A  и  М_А зависят от ряда факторов , в том числе от  ,плотности воздуха , скорости воздушного потока , аэродинамической формы ракеты и т.д.

             Для того , чтобы было удобно составлять уравнения принято R_A  и  М_А  раскладывать по осям координатной скоростной (поточной) системы .

             Известно , что R_A в наибольшей степени , кроме формы ракеты , зависит от угла атаки и от угла скольжения  .

§  По осям скоростной системы координат R_A есть :

§  По осям связанной системы координат R_A есть :

Проекция R_A на поточную ось ракеты Ox_n всегда отрицательна и носит название силы лобового сопротивления () .

 - подъемная сила ;

 - боковая подъемная сила .

Проекция R_A :  Х₁ — осевая сила ; Y₁ — нормальная сила ; Z₁ — боковая нормальная сила .

            Баллистическая ракета является аэродинамически осесимметричным телом . Если ось ракеты направлена по вектору скорости (т.е. ) , то обтекание ракеты воздушным потоком будет симметричным относительно плоскости , проходящую через продольную ось ракеты , т.е. силы :  Y₁=Y=0  ;  Z₁=Z=0  .

            Если ось ракеты образует с вектором скорости некоторый угол , то обтекание ракеты воздушным потоком будет симметричным относительно плоскости , проходящей через ось ракеты и вектор скорости . При этом R_A  и ее составляющие (X,X₁,Y,Y₁) будут лежать в этой плоскости , следовательно что для аэродинамики симметричной ракеты зависимости силы Z(Z₁) от угла скольжения  аналогичны зависимостям силы Y(Y₁) от угла атаки  . На основании теории аэродинамического подобия проекции аэродинамической силы на оси координат (связанной или скоростной) будут равны .

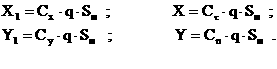         , где

 - скоростной напор действующий на ракету ;

    - плотность на высоте полета ;

V  -скорость ракеты ;

S_м – характерная площадь ЛА (площадь Миделя) ;

  ; D_p –диаметр цилиндрической части ракеты ;

 - безразмерные аэродинамические коэффициенты .

Аэродинамические коэффициенты зависят от формы ракеты , от ориентации ракеты , относительно вектора воздушной скорости (т.е. от ) , а также от критериев аэродинамического подобия .

            Критерии аэродинамического подобия :

§  Число Маха     ;

§  Число Рейнольдса    ;

а=а(h)  — скорость воздуха в воздушной среде ;

l  -характерный размер ЛА (для ракеты — длина ракеты) ;

  - кинематический коэффициент вязкости воздуха .