Лекции для студентов

Лекция по “Теории полёта”. Часть 1

Форма Земли

            Земля представляет собой геометрическое тело сложной формы .Поверхность Земли , со всеми ее неровностями называется физической поверхностью Земли . Из геометрических тел , описывающих форму Земли наиболее близко к реальной Земле подходит геоид .

          

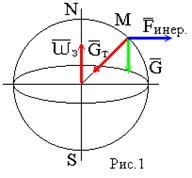
  Геоид - представляет собой тело ограниченное уровенной поверхностью силы тяжести ,  совпадающей с поверхностью океана (невозмущенной приливами и волнами) и продолженной под материками . Поверхность геоида непрерывно замкнута и не имеет резких перегибов и складок .

                        F_инер     -сила инерции

                        Gт       -сила притяжения

                        G         -сила тяжести

Примечание : экспериментальным путем невозможно отделить центробежную силу инерции от силы земного притяжения . Известно , что массы пород внутри Земли распределены неравномерно и направление силы тяжести в различных точках Земли зависит от этого распределения , поэтому поверхность геоида является весьма сложной и не имеет математического описания .

            В первом приближении Землю можно считать шаром , объем которого равен объему Земли , а радиус

            В большинстве случаев с достаточной для практического использования точностью геоид можно заменить эллипсоидом вращения , полученным вращением эллипса вокруг малой оси . Эллипсоид , который наилучшим образом приближается к поверхности реального геоида носит название общего земного эллипсоида .

            Он определяется из следующих условий :

§  Центр эллипсоида совпадает с центром Земли , а плоскость его экватора совпадает с плоскостью экватора Земли .

§  Объемы эллипсоида и геоида равны .

§  Сумма квадратов отклонений (по высоте) к поверхности общего земного эллипсоида от поверхности геоида должна быть минимальной .

 

В настоящее время приняты размеры общего земного эллипсоида :

§  Большая полуось (радиус экватора)

а=6378137 м

§  Малая полуось

b=6356752 м

  -сжатие эллипсоида ;

           

            По мнению ряда ученых поверхность даже самого точного эллипсоида ,правильно ориентированного по отношению к Земле может отклоняться от поверхности геоида на величины  м .

            В некоторых странах , больших по площади , с целью уменьшения геодезических ошибок , появляющихся от замены геоида общим земным эллипсоидом вводят понятие о референс эллипсоиде . Им называют эллипсоид вращения с соответствующими размерами , определенным образом ориентированным к поверхности Земли и к поверхности которого относятся результаты геодезических работ на рассматриваемом участке земной поверхности в данном государстве .

            На территории СССР за размеры референс эллипсоида приняты размеры Красовского :

а=6378245 м ;

b=6357520 м ;

 .