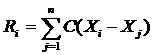Лекции для студентов

Лекции по системному анализу в чрезвычайных ситуациях. Часть 1

2.2. Порядковые шкалы

В случаях, когда наблюдаемый (измеряемый) признак состояния имеет природу, не только позволяющую отождествить состояние с одним из классов эквивалентности, но и дающую возможность в какой-то степени сравнивать разные классы, для измерения можно выбрать более сильную шкалу, чем номинальная. Однако это усиление измерительной шкалы зависит от того, какие именно отношения между классами существуют в действительности, поэтому существуют и измерительные шкалы разной силы.

Порядковая (или ранговая) шкала является следующей по силе за номинальной. Эта шкала применима, если кроме аксиом тождества (1) — (3) классы эквивалентности удовлетворяют следующим аксиомам упорядоченности:

4) Если А > В, то В < А

5) Если А > В и В > С, то А > С.

Обозначив такие классы символами, и установив между этими символами те же отношения порядка, мы получим шкалу простого порядка (нумерация очередности, призовые места в конкурсе, воинские и ученые звания и т.п.).

Иногда бывает, что некоторые пары не упорядочиваются по предпочтению и считаются равными, тогда имеем аксиомы:

4¢) либо А £ В, либо А ³ В (если А ³ В, то В £ А)

5¢ ) Если А ³ В и В ³ С, то А ³ С.

Шкала, соответствующая аксиомам 4’, 5’ — это так называемая шкала «слабого порядка». Пример: степень родства (мать=отец > сын=дочь, дядя=тетя > брат=сестра и т.п.)

Бывают ситуации, когда некоторые пары классов несравнимы между собой, т.е. ни А £ В, ни В £ А. Для таких случаев используется шкала частичного порядка (в социологических исследованиях субъективных предпочтений — покупательский спрос, любимые занятия и т.п.) (В лабораторной работе №1 — показатели выбора городов).

Характерная особенность порядковых шкал – это то, что отношения порядка ничего не говорят о дистанции между сравниваемыми классами. Поэтому порядковые данные также нельзя рассматривать как числа, как и номинальные, даже если они изображены цифрами. Над ними, следовательно, нельзя выполнять действия, приводящие к получению разных результатов при преобразовании шкалы, не нарушающем порядка (Х : 1 2 3 4 5) Þ (Х¹ : 1 4 6 8 10).

Например, нельзя вычислять выборочное среднее порядковых измерений,так как переход к монотонно преоразованной шкале x’ =f(x) при усреднении даст т.е. т.к. .

Однако, допустима операция, позволяющая установить, какое из 2-х наблюдаемых Х_i или Х_j предпочтительнее и определить ранг объекта. Поэтому порядковая шкала называется еще и ранговой. Пусть С(t) — индикатор положительных чисел, где t = X_i — X_j 

0 : t < 0;

 C(t) = 1 : t ³ 0;

Тогда

 — ранг i-го объекта.

1 < R_i £ n.

 

Важно! Даже в тех случаях, когда состояния, допускающие только порядковые сравнения, в эксперименте измеряются через величины, связанные с ними косвенно, но фиксируемые в числовых шкалах, эти измерения все равно остаются измерениями в порядковой шкале.

Например, при испытании умственных способностей измеряется время, затрачиваемое испытуемым на решение тестовой задачи. Но, хотя время измеряется в числовой шкале, здесь, как мера интеллекта оно его измерение принадлежит к порядковой шкале.