Лекции для студентов

Лекции по системному анализу в чрезвычайных ситуациях. Часть 1

2. Операторы системы

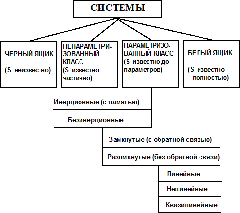
Оператором S системы называется связь между входными и выходными переменными. Соответственно, то особенностям операторов системы классифицируются следующим образом (рис.3).

На 1-м уровне здесь располагаются классы систем, отличающиеся степенью известности оператора S.

Рис.3

Здесь второй блок 1-го уровня (непараметризованный класс) соответствует ситуациям с очень скудной априорной информацией об S. Может, например, быть известно, что в соотношении Y = S (x) функция S непрерывна, монотонна или симметрична, но никаких конкретных данных о функциональном характере этой зависимости нет.

Третий блок 1-го уровня соответствует ситуации, когда мы можем записать зависимость y(x) от x(t) в явной форме с точностью до конечного числа параметров q = (q₁ … q_к), т.е. y(t) = S(x(×), q). Пример: S = Jⁿ — закон Стивенса , Закон Вебера-Фехнера S = KlnJ + C.

Большие и сложные системы. Теперь можно вновь вернуться к определению больших и сложных систем и уточнить их.

Большие системы — системы, моделирование которых затруднительно вследствие их размерности. Существуют два способа перевода их в малые:

1) разработка более мощных ЭВМ;

2) декомпозиция многомерной задачи на совокупность связанных задач меньшей размерности.

Сложные системы — системы, в моделях которых не хватает информации для эффективного управления.

Действительно, признак простоты системы — это достаточность информации для управления. Если же полученное с помощью модели управления приводит к неожиданным, непредвиденным или нежелательным результатам, т.е. отличающимися от предсказанных моделью, это может быть объяснено недостатком информации и интерпретироваться как сложность системы.

Таким образом, свойство простоты или сложности управляемой системы является свернутым отношением между нею и управляющей системой, точнее, между системой и ее моделью. Это отношение объективно (примеры: кодовый замок, родной язык, умение обращаться с компьютером, водить автомобиль и т.п.).

Считается также, что сложную систему можно охарактеризовать тремя основными принципами:

1) свойством робастности (сохранения частичной работоспособности при отказе отдельных элементов или подсистем, что объясняется функциональной избыточностью сложной системы (простая система может находиться лишь в одном из двух состояний (работоспособности или полного отказа);

2) большим числом неоднородных (разных по типу) связей;

3) интегративной целостностью (эмерджентностью), которая достигается за счет обратных связей, играющих важнейшую роль в управлении сложной системой.

В отношении информации можно сказать то, что структурная сложность системы должна быть пропорциональна объему информации, необходимой для ее описания (т.е. снятия неопределенности). В этом случае общее количество информации о системе S, в которой априорная вероятность появления j-го свойства равна p(y_i), определяется соотношением для количества информации (энтропийный подход):

Y = — S p(y_i)log₂(p(y_i))/

Такая сложность называется также дескриптивной (описательной). Одним из способов описания такой сложности является оценка числа элементов, входящих в систему (переменных, состояний, компонентов) и разнообразия связей между ними.

В общей теории систем утверждается, что не существует систем обработки данных, которые могли бы обработать > 2×10⁵⁴⁷бит/(сек×г). Задачи, которые требую скорости более 10⁵⁹³ бит/(сек×г) (предел Бремермана — такое количество информации может обработать компьютер с массой, равной массе Земли за 4,5 млрд. лет), называются трансвычислительными.

Возможны два способа перевода сложной системы в более простую:

1) получение недостающей информации (основная задача науки);

2) смена цели.

Классификация по отношению к информационным ресурсам может быть развита и дополнена. Например, есть предложения выделить в отдельный класс «очень сложные системы (мозг, экономика и т.п.).

Не следует путать понятия сложная система и большая система: первое связано с материальными ресурсами, размерностью, второе — с информацией. Таким образом, между большими, малыми, простыми и сложными системами возможны все четыре комбинации (см. рисунок).

Итак, на основании рассмотренного в этой и в предыдущих лекциях можно сделать следующий вывод.

Если признать, что искусственная система остается системой, даже если ее цель неизвестна, а природа объективно системна, т.е. естественные объекты структурированы, упорядочены и имеют объективные цели.

Следует, что «не систем» в мире вообще не существует. Мы можем рассматривать некоторый объект, не считаясь с его системностью, но рано или поздно это выльется в появление проблем.

Характерные же различия между всевозможными системами учитываются с помощью классификаций систем.

При управлении системой выделяют следующие аспекты:

а) описание природы системы S;

б) задание типов переменных X, Y, Z;

в) конкретизация типа оператора S;

г) описание способа управления (получения U);

д) задание условий получения U (обеспеченности управления ресурсами).

Каждый из этих аспектов служит основой построения классификаций систем.

Контрольные вопросы

1. Какая проблема возникает при переносе понятия системы на естественные объекты?

1. Можно ли утверждать, что объект (естественный или искусственный) не является системой, если его цель неизвестна?
2. Что такое оператор системы?
3. Что такое «переменные системы»? Какие виды переменных, служащие основанием для классификации Вы знаете?
4. Что означает развитие модели от «черного ящика» до «белого ящика».
5. Какие промежуточные между черным и белым ящиком классы моделей систем Вы можете назвать?
6. Чем отличаются инерционные и безинерционные системы?
7. Какие особенности управления дают основания для различения программного управления, регулирования, параметрической адаптации, структурной адаптации?
8. Чем отличается большая система от сложной?
9. Что такое сложность систем: отношение между системой и ее моделью или атрибут самой системы?