Лекции по системному анализу в чрезвычайных ситуациях. Часть 1
- Лекции по системному анализу в чрезвычайных ситуациях. Часть 1
- 1.2. Познавательные и прагматические модели
- 1.3. Статические и динамические модели
- 1.4. Классификация моделей по способу воплощения
- 1.5. Знаковые модели и сигналы
- 1.6. Условия реализации модельных свойств
- Лекция 2. Модели систем
- 2.1. Система как средство достижения цели
- 2.2. Модель «черного ящика»
- 2.3. Модель состава системы
- 2.4. Модель структуры системы
- 2.5. Структурная схема системы. Графы
- 2.6. Динамические модели систем.
- Лекция 3. Классификация систем.
- 3.1. Переменные системы
- 3.2. Операторы системы
- Лекция 4. Системы с управлением
- 4.2. Гомеостазис системы
- 4.3. Ресурсы управления
- Лекция 5. роль измерений при моделировании систем
- 5.2. Измерительные шкалы
- 5.2.1. Шкалы наименований
- 5.2.2. Порядковые шкалы
- 5.2.3. Модифицированные порядковые шкалы
- 5.2.4. Шкалы интервалов
- 5.2.5. Шкалы отношений
- 5.2.5. Шкалы разностей
- 5.2.6. Абсолютная шкала
- 5.2.7. Замечания по применимости шкал при измерении изучаемых объектов
|
Рис.5 |
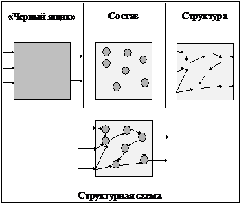
На основании рассмотренного ранее можно дать второе, более полное определение системы, охватывающие и модель «черного ящика» и модель состава и модель структуры.
Система — есть совокупность взаимосвязанных элементов, обособленная от среды и взаимодействующая с ней как целое.
Модели «черного ящика», состава и структуры вместе образуют структурную схему системы («белый ящик», «прозрачный» ящик). Все рассмотренные виды моделей схематично изображены на рис. 5.
На рис. 6 в качестве примера приведена структурная схема часов.
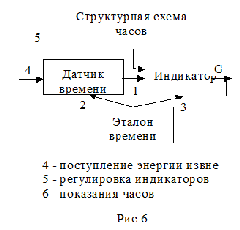Если отвлечься от конкретного содержания элементов систем, видно, что все структурные схемы имеют общее, поэтому они рассматриваются также как особый объект математических исследований и являются предметом специальной науки, именуемой теорией графов (раздел математики).
Действительно, если абстрагироваться от содержательной стороны структурных схем, получится схема, в которой обозначается только наличие элементов и связей между ними и, если необходимо, разница между элементами и между связями. Такая схема называется графом.
(Как самостоятельная дисциплина теория графов сформировалась в 30-е годы 20-го века, хотя начало теории графов было положено еще в 1736 г. А.Эйлером в его знаменитом рассуждении о кенигсбергских мостах).
Граф состоит из обозначений элементов произвольной природы, называющейся вершинами, и обозначений связей между ними, называющимися ребрами.
Ei — вершины графа
Например — транспортная сеть.
Ei — пункты.
Если движение двустороннее — линии без стрелок, одностороннее — со стрелками (ориентированный граф). Граф может иметь и изолированную вершину. Подробнее о применении графов при моделировании систем, в частности при решении задач безопасности жизнедеятельности мы будем говорить во второй части нашего курса.
