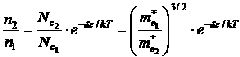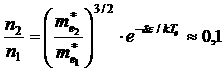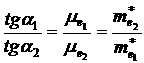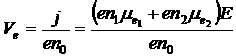Физика полупроводников. Лекция 4
- Физика полупроводников. Лекция 4
- §2. Дрейфовая электропроводность в полупроводнике.
- §3. Диффузионная электропроводность в полупроводнике. Соотношения Эйнштейна.
- §4. Температурная зависимость подвижности носителей заряда в полупроводниках.
- §5. Температурная зависимость подвижности при смешанном механизме рассеяния носителей заряда.
- §6. Разогрев носителей заряда в сильных электрических полях.
- §7. Термоэлектронная ионизация Френкеля.
- §8. Ударная ионизация в полупроводниках.
- §9. Туннельный эффект в полупроводниках (электростатическая ионизация Зинера).
- §10. Отрицательная дифференциальная проводимость (ОДП) полупроводников с двух долинной зонной структурой.
- §11. Колебания тока в двухдолинных полупроводниках (эффект Ганна).
- §12. Токи ограниченные пространственным зарядом (ТОПЗ) в полупроводниках без “ловушек”.
- §13. ТОПЗ в полупроводниках с ловушками.
- §14. Основные свойства сверхпроводящего состояния твердых тел.
- §15. Природа сверхпроводимости (теория БКШ).
- §16. Применение сверхпроводимости.
§10. Отрицательная дифференциальная проводимость (ОДП) полупроводников с двух долинной зонной структурой.
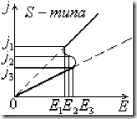 На ВАХ
На ВАХ ![]() ряда полупроводников в сильных электрических полях наблюдаются участки ОДП (когда
ряда полупроводников в сильных электрических полях наблюдаются участки ОДП (когда ![]() ) N или S типа.
) N или S типа.
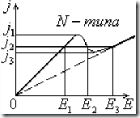 На образах с ОДП N-типа напряженность электрического поля в области токов
На образах с ОДП N-типа напряженность электрического поля в области токов ![]() является многозначной функцией плотности тока. На образах с ОДП S-типа плотность тока в области токов
является многозначной функцией плотности тока. На образах с ОДП S-типа плотность тока в области токов ![]() является функцией напряженности электрического поля. Будем рассматривать ВАХ с ОДП N-типа. Одной из возможных причин ОДП N-типа является изменение подвижности носителей заряда в результате междолинных переходах в сильных электрических полях. Для определенности будем рассматривать полупроводник
является функцией напряженности электрического поля. Будем рассматривать ВАХ с ОДП N-типа. Одной из возможных причин ОДП N-типа является изменение подвижности носителей заряда в результате междолинных переходах в сильных электрических полях. Для определенности будем рассматривать полупроводник ![]() — типа. Представим, что в его зоне проводимости имеется по крайне мере два энергетических минимума (две долины), разделенных небольшим интервалом энергий
— типа. Представим, что в его зоне проводимости имеется по крайне мере два энергетических минимума (две долины), разделенных небольшим интервалом энергий ![]() . Например, в кристаллах арсенида галия (GaAs)
. Например, в кристаллах арсенида галия (GaAs) ![]() — типа в зоне проводимости основной минимум лежит в центре зоны Бриллюэна (
— типа в зоне проводимости основной минимум лежит в центре зоны Бриллюэна (![]() ), а второй минимум лежит на оси [100] на расстоянии от центра зоны Бриллюэна равном
), а второй минимум лежит на оси [100] на расстоянии от центра зоны Бриллюэна равном ![]() , a — постоянная решетки. Дно зоны проводимости определяется абсолютным минимумом первой долины.
, a — постоянная решетки. Дно зоны проводимости определяется абсолютным минимумом первой долины.
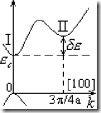 Для GaAs:
Для GaAs: ![]() ,
, ![]() (легкие электроны),
(легкие электроны), ![]() (тяжелые электроны),
(тяжелые электроны), 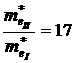 . Следовательно, подвижность электронов:
. Следовательно, подвижность электронов: 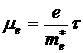 в первой долине будет значительно больше, чем во второй
в первой долине будет значительно больше, чем во второй ![]() . В нормальных условиях (слабые электрические поля) очевидно электронная температура рана
. В нормальных условиях (слабые электрические поля) очевидно электронная температура рана ![]() (не разогретые электроны). Их концентрация в долинах будет определяться соотношением:
(не разогретые электроны). Их концентрация в долинах будет определяться соотношением:
При ![]() для GaAs
для GaAs ![]() , т.е. практически все электроны будут находиться в первой долине. Будем считать, что концентрация электронов не зависит от электрического поля.
, т.е. практически все электроны будут находиться в первой долине. Будем считать, что концентрация электронов не зависит от электрического поля.
Электрическое поле только перераспределяет электроны между первой и второй долиной. Значит, в слабых электрических полях ![]() и электропроводность полупроводника будет равна:
и электропроводность полупроводника будет равна:
Если подвижность носителей заряда достаточно велика, то в сильных электрических полях они заметно разогреваются (неравновесные условия, ![]() ). Например, в кристалле GaAs
). Например, в кристалле GaAs ![]() — типа при T = 3000 K и
— типа при T = 3000 K и ![]()
![]() , то Te = 6000 K. Тогда в неравновесных условиях:
, то Te = 6000 K. Тогда в неравновесных условиях:
Значит в этих условиях 10% электронов переходят во вторую долину. С увеличением ![]() все большая часть электронов будет переходить с первой во вторую долину. Тогда ВАХ такого образа буде определяться соотношением:
все большая часть электронов будет переходить с первой во вторую долину. Тогда ВАХ такого образа буде определяться соотношением:
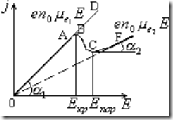
![]() , проводимость при равновесных условиях с ростом
, проводимость при равновесных условиях с ростом ![]() увеличивается, и следовательно
увеличивается, и следовательно ![]() будет увеличиваться и может случиться так, что
будет увеличиваться и может случиться так, что ![]() будет падать быстрее, чем растет поле, тогда на ВАХ появляется падающий участок (ОДП). В слабых электрических полях
будет падать быстрее, чем растет поле, тогда на ВАХ появляется падающий участок (ОДП). В слабых электрических полях ![]() и тогда
и тогда
В очень сильных электрических полях: ![]() ,
, ![]() , тогда
, тогда
В промежуточной области рост тока ![]() будет замедлятся, и когда большая часть электронов будет переходить во вторую долину ток будет падать с ростом
будет замедлятся, и когда большая часть электронов будет переходить во вторую долину ток будет падать с ростом ![]() (участок BC).
(участок BC).
Зная из эффекта Холла подвижность в первой долине можно определить подвижность электронов во второй долине.
ОДП N-типа в двухдолинных полупроводниках соответствует отрицательной дифференциальной проводимости электронов 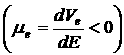 . Действительно, среднее значение дрейфовой скорости электронов будет определяться из соотношения:
. Действительно, среднее значение дрейфовой скорости электронов будет определяться из соотношения:
В очень слабых электрических полях ![]() ,
, ![]() , тогда
, тогда
В очень сильных электрических полях ![]() ,
, ![]() , тогда
, тогда
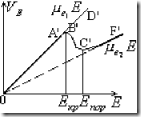 Тогда зависимость средней дрейфовой скорости от Е в двухдолинных полупроводниках будет иметь вид:
Тогда зависимость средней дрейфовой скорости от Е в двухдолинных полупроводниках будет иметь вид:
Таким образом, в двухдолинных полупроводниках N-образная ВАХ связана с N-образным характером зависимости средней дрейфовой скорости ![]() от Е.
от Е.