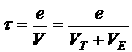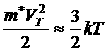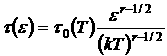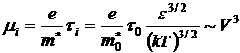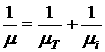Лекции для студентов

Физика полупроводников. Лекция 4

§6. Разогрев носителей заряда в сильных электрических полях.

В слабых электрических полях подвижность и концентрация носителей заряда не зависит от напряженности внешнего поля, т.е. выполняется закон Ома:

,

Этому условию соответствует равновесное состояние, когда кристаллическая решетка получает от свободных носителей заряда столько энергии, сколько им отдает. В равновесном состоянии температура носителей заряда совпадает с температурой кристаллической решетки . При наложении сильного электрического поля стационарное состояние не сразу, следовательно, после включения внешнего поля со временем возрастает энергия свободных носителей заряда, получаемая от внешнего электрического поля. На этом этапе носители заряда уже не находятся в равновесии с кристаллической решеткой, их температура выше чем температура решетки . В этот период со временем возрастает передача энергии от носителей заряда к кристаллической решетке и только когда устанавливается стационарное состояние, количество энергии получаемой носителями заряда от поля полностью передается кристаллической решетки в виде тепла. В этих условиях устанавливается стационарная разность температур . Рассчитаем энергию, которую передает электрическое поле носителей заряда (электроны) в единицу объема за единицу времени:

(1)

(1) — закон Джоуля-Ленца в дифференциальной форме.

В сильных электрических полях может стать сопоставимой с тепловой скоростью , . Это особенно актуально для полупроводника имеющую высокую подвижность носителей заряда. В этом случае время свободного пробега носителей заряда равно:

В этом случае время свободного пробега, а следовательно и подвижность носителей заряда является функцией электрического поля. Зная подвижность можно определить электронную температуру из соотношения:

Температуру кристаллической решетки можно определить из соотношения:

В зависимости от механизма рассеяния сильное электрическое поле может уменьшать или увеличивать подвижность носителей заряда. Теоретическими расчетами показано, что при рассеянии носителей заряда на ионах примеси, на нейтральной примеси, на незаряженных вакансиях, на колебаниях решетки время свободного пробега можно представить в виде:

 — полная энергия носителей заряда,  — коэффициент зависящий от механизма рассеяния и температуры решетки,  — фактор рассеяния, значение которого приведены в таблице.

Механизм рассеяния	r
На тепловых (акустических) колебаниях решетки	0
На незаряженных вакансиях	0
На оптических колебаниях	½
На оптических колебаниях	1
На нейтральной примеси	½
На ионах примеси	2

,  — температура Дебая.

Рассмотрим случай когда в кристалле имеет место рассеяние носителей заряда, например, на ионах примеси и тепловых колебаниях решетки (Ge, Si). При рассеянии на тепловых колебаниях решетки подвижность равна:

(3)

При рассеянии на ионах примеси подвижность равна:

(4)

При всех механизмах рассеяния скорость носителей заряда равна:

Скорость растет с ростом , значит будет падать с ростом , а будет возрастать. Известно, что при смешанном механизме рассеяния эффективная подвижность определяется соотношением:

(5)

При низких температурах, очевидно, будет доминировать рассеяние на ионах примеси, тогда полевая зависимость эффективной подвижности будет выглядеть, так как показано на рисунке. При больших значениях 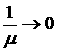, тогда .

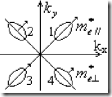Сильное электрическое поле может привести и к некоторым другим физическим явлениям, например, к ионизации электропроводимости в кристалле кубической структуры. В курсе кристаллофизики будет показано, что в слабых электрических полях электропроводность в кристаллах кубической системы является изотропной величиной, одинаковая во всех трех направлениях кристалла. Для того чтобы понять влияние сильного электрического поля на электропроводность кристалла Ge спроектируем его эллипсоиды энергии на плоскость рисунка.

Стрелками указаны направления электрических полей. Эффективная масса электронов, движущихся в направлении поля, будут различны для разных эллипсоидов. Для эллипсоидов 1, 3 эффективная масса продольная, для 2, 4 поперечная. Ускорение электронов будет различно для разных эллипсоидов. Также будут различны подвижность, температура в различных эллипсоидах, концентрация и плотность также будет различна. Суммирование по всем эллипсоидам не устраняет анизотропию электропроводности.