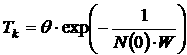Лекции для студентов

Физика полупроводников. Лекция 4

§15. Природа сверхпроводимости (теория БКШ).

Природа сверхпроводимости стала понятной благодаря микроскопической теории, созданной в 1957 г. Бардиным, Купером и Шлиффером. В основе теории БКШ лежит представление о том, что между электронами проводимости кристалла могут действовать не только силы отталкивания, но и силы притяжения, возникающие вследствие поляризации решетки. Электроны, движущиеся в кристаллической решетке притягивают к себе положительные ионы и тем самым создают вдоль своего пути движения избыточный положительный заряд, к которому могут быть притянуты другие электроны. Это эквивалентно возникновению силы притяжения между электронами, но действующей не непосредственно, а через поляризованную решетку, поэтому сверхпроводимость наблюдается у тех металлов, у которых имеет место сильное взаимодействие с кристаллической решеткой, а значит, такие металлы в обычных условиях имеют относительно низкую электропроводность. Например, у хорошо проводящих металлов Cu, Ag, Au сверхпроводимость не наблюдается.

Преобладание в определенных условиях сил притяжения между электронами над силой их кулоновского отталкивания приводит к понижению энергии кристалла. Расчетами Купера показано, что энергетически наиболее выгодным является образование из электронов электронных пар, причем таких, которые образованы из электронов, обладающих противоположными спинами, равными по величине, но противоположными по направлению импульсами. Такие электроны называются куперовскими. В них объединяются два электрона, находящихся с разных сторон от ближайшего положительно заряженного иона. Взаимодействие электронов в паре происходит путем обмена фононами — квантами колебания кристаллической решетки, таким образом, куперовские пары имеют заряд –2е, нулевое значение спина и нулевое значение импульса в отсутствии внешнего электрического поля (базоны). Обладая нулевым значением спина, куперовские пары подчиняются статистике Бозе — Эйнштейна. Переход значительного числа электронных пар в состояние с нулевым импульсом называется бозеконденсацией по аналогии с конденсацией молекул пара в жидкость при низких температурах. Так как сила притяжения между электронами в куперовской паре относительно слаба, то спаренные электроны не “слипаются” друг с другом, они находятся на достаточно большом расстоянии друг от друга: . Следовательно, объем занимаемый одной куперовской парой будет равен .

В металлах куперовские пары могут объединяться только те электроны, которые могут возбуждаться и менять свое состояние. Такими электронами являются электроны с уровня Ферми, ответственные за электропроводность металла. Их концентрация , следовательно, в объеме, занимаемой одной куперовской парой будет находиться других куперовских пар.

Пространственное перекрытие огромного числа куперовских пар приводит к строгой взаимной корреляции (согласованности) их движения под действием внешнего электрического поля. Все они приобретают один и тот же импульс и движутся как единый коллектив в одном и том же направлении с некоторой дрейфовой скоростью. При этом поведение куперовских пар отличается от поведения обычных электронов, т.е. электронов, находящихся в нормальном состоянии. Нормальные электроны испытывают рассеяние на колебаниях кристаллической решетки и других дефектах решетки. Это приводит к хаотизации их движения, что является причиной возникновения электрического сопротивления. Куперовские пары пока они не разорваны, не могут рассеиваться на дефектах решетки, так как выход любой из них из строго коррелированного коллектива мало вероятен. При этом вырвать куперовскую пару из такого коллектива тем труднее, чем больше таких пар. Любое нарушение в движении данной пары должно сказываться на свойствах всей совокупности пар. Пару можно вырвать из коллектива лишь разрушив ее, однако, при очень низких температурах число фононов, имеющих для этого энергию, исключительно мало. Поэтому подавляющее число образовавшихся куперовских пар сохраняются не разрушенными. Не испытывая рассеяние при своем направленном движении и имея заряд –2е, они обуславливают появление сверхпроводящего тока.

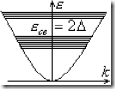Куперовские пары, являясь базонами, размещаются на одном уровне, расположенном ниже уровня Ферми на расстоянии энергетическом . Очевидно, чтобы разорвать куперовскую пару, надо затратить энергию: , т.е. энергию на каждый электрон. Это означает, что нормальное состояние в сверхпроводнике отделено от сверхпроводящего энергетической щелью, равной . С ростом температуры кристалла ширина щели сужается, а при энергетическая щель сужается до нуля и сверхпроводящее состояние разрушается, и все электроны становятся нормальными. Из теории БКШ следует, что температура перехода в сверхпроводящее состояние связано следующим соотношением с параметрами кристалла:

 — некоторая характеристическая температура для материал проводника (температура Дебая). .  — плотность состояний вблизи уровня Ферми,  — среднее значение матричного элемента взаимодействия двух электронов. Чтобы была высокой, произведение должно быть большим. Много долинные полупроводники обладают большей плотностью состояний. Если у полупроводника несколько минимумов, то электрон может перейти в любой минимум. Сверхпроводящие полупроводники GeTe, SnTe имеют 12 долин в зонах проводимости, они лежат в направлениях зоны Бриллюэна.