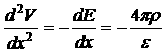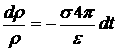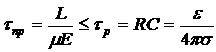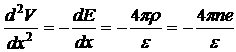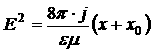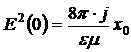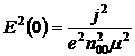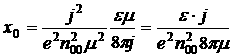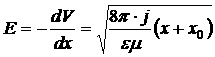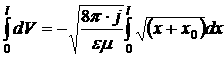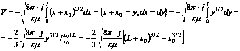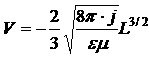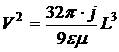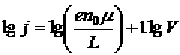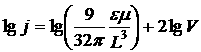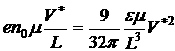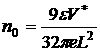Лекции для студентов

Физика полупроводников. Лекция 4

Страница 12 из 16

§12. Токи ограниченные пространственным зарядом (ТОПЗ) в полупроводниках без “ловушек”.

Омический ток протекает в условиях электро нейтральности каждой физически малой области полупроводника. В этих условиях отсутствует накопление электрических зарядов внутри полупроводника. В диэлектриках или высокомных полупроводниках отсутствуют или находятся в малом количестве свободные носители заряда. Поэтому проводимостью таких материалов, как и вакуумного промежутка можно управлять путем введения (инжекции) в них избыточных свободных носителей заряда. Избыточные носители заряда создают объемный заряд, электрическое поле которого ограничивает величину тока через полупроводник.

Одним из способов введения избыточных носителей заряда является создание в полупроводнике омического контакта. Такой контакт можно создать при условии, что термодинамическая работа выхода металла меньше, чем у полупроводника. Термодинамическая работа выхода равна разности между минимальной энергии электрона в вакууме и Ферми — энергией электронов внутри твердого тела. При таком контакте электроны металла диффундируют в объем полупроводника, создавая избыточный заряд электронов, который создает электрическое поле внутри полупроводника независимо от того, приложено ли к полупроводнику внешнее электрическое поле. В результате такого перехода узкая приконтактная поверхность металла заряжается положительно, а приконтактная область полупроводника — отрицательно. Электрическое поле объемного заряда в полупроводнике будет возрастать до тех пор, пока не будет скомпенсировано полем контактной разности потенциалов (Контактным полем) :

Поле объемного заряда проникает тем глубже в полупроводник, чем меньше концентрация его собственных носителей заряда. Поле объемного заряда увеличивает энергию электронов полупроводника вблизи его контакта. В связи с этим зоны полупроводника вблизи контакта загибаются вверх. Приведенная диаграмма соответствует стационарному состоянию, когда число электронов, перемещающихся слева направо равно обратному потоку. В этих условиях уровень химического потенциала на обоих материалах одинаков.

Теперь приложим к полупроводнику внешнее электрическое поле полярностью, как показано на рисунке. Все внешнее поле будет приложено к полупроводнику (так как в металле сопротивление маленькое). Распределение 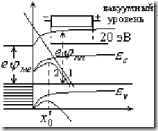потенциальной энергии электронов во внешнем электрическом поле показано прямой 1. Внешнее электрическое поле полностью компенсирует поле объемного заряда в некоторой точке . Дно зоны проводимости полупроводника во внешнем электрическом поле выглядит как кривая 2. Точка местоположение “виртуального катода”. Только те электроны, значения энергий которых выше энергии потенциального барьера в точке будут участвовать в переносе электрического тока через полупроводник. С ростом внешнего поля будет уменьшаться высота потенциального барьера, и все большая часть электронов будет участвовать в переносе электрического тока. Но пока время пролета электронов через полупроводник:

,

больше времени жизни избыточных электронов, ток через полупроводник будет являться омическим. Только тогда, когда заряд инжектированных из металла электронов заполняет всю область полупроводника, с этих пор через полупроводник будет протекать ограниченный ТОПЗ. Это случиться когда время пролета станет . — время диэлектрической релаксации избыточных электронов (время жизни избыточных электронов).

Уравнение непрерывности:

Уравнение Пуассона:

, или ()

Из первого уравнения получаем:

,

()

Приравняем () и ():

,

— время жизни носителей избыточного заряда. Как только 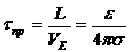, тогда будет протекать ТОПЗ. Для создания режима ТОПЗ необходимо выполнение неравенства:

Отсюда следует, что режим ТОПЗ можно создать в полупроводниках: высокомных ( — мало) в сильных электрических полях и при малом межэлектродном расстоянии L, иными словами, для наблюдений ТОПЗ используют тонкопленочные образцы, в которых можно легко создать сильные электрические поля, например: , , . Найдем вид ВАХ для ТОПЗ в случае, если в полупроводнике нет мелких центров, захватывающих свободные носители заряда (нет ловушек). При наличии омического контакта ток в сильных электрических полях будет состоять из суммы дрейфового и диффузионного тока:

(1)

Из соотношений Эйнштейна:

Из уравнения Пуассона:

(2)

Из (2) следует:

Подставим и в (1):

(3)

Проинтегрируем (3) по x (учтем, что ):

В экстремальных условиях в большинстве случаев выполняется неравенство:

(4)

Действительно: , тогда . Значит неравенство (4) будет иметь место, если (при , )

С учетом указанного неравенства:

,

(5)

Под понимается напряженность электрического поля, созданная объемным зарядом и внешним полем, таким образом, она является функцией х, т.е. , как и следует из (5). В точке :

(6)

Плотность тока в точке :

— концентрация электронов в полупроводнике вблизи границы с металлом. Из последнего соотношения следует:

(7)

Из (6) и (7) определяем, что:

(8)

Запишем уравнение Пуассона с учетом (5):

Проинтегрируем последнее выражение:

,

Проанализировав соотношение для можно показать, что в случае малых токов величина сопоставима с концентрацией электронов в металле, т.е. она является большой величиной для полупроводника, поэтому , следовательно:

Возведем в квадрат последнее выражение:

, (9)

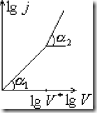
(9) — формула Мотта и Герни, определяет собой ВАХ безловушечного ТОПЗ. Из (9) следует, что ТОПЗ зависит от внешнего напряжения по квадратичному закону. При этом ТОПЗ при прочих равных условиях обратно пропорционален кубу толщины диэлектрической пленки. Если до приложенного внешнего напряжения в полупроводнике имелись свободные электроны с концентрацией (равновесные электроны), то в слабых электрических полях будет иметь место омический ток, переносимый равновесными носителями заряда. А в очень сильных электрических полях будет протекать ТОПЗ, связанный с электронами, инжектированными из контакта. А в промежуточной области напряженности электрического поля ток будет равным сумме омического тока плюс ТОПЗ. Очевидно, в области напряжения омический ток будет совпадать с ТОПЗ. В омической области: