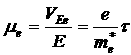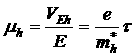Физика полупроводников. Лекция 4
- Физика полупроводников. Лекция 4
- §2. Дрейфовая электропроводность в полупроводнике.
- §3. Диффузионная электропроводность в полупроводнике. Соотношения Эйнштейна.
- §4. Температурная зависимость подвижности носителей заряда в полупроводниках.
- §5. Температурная зависимость подвижности при смешанном механизме рассеяния носителей заряда.
- §6. Разогрев носителей заряда в сильных электрических полях.
- §7. Термоэлектронная ионизация Френкеля.
- §8. Ударная ионизация в полупроводниках.
- §9. Туннельный эффект в полупроводниках (электростатическая ионизация Зинера).
- §10. Отрицательная дифференциальная проводимость (ОДП) полупроводников с двух долинной зонной структурой.
- §11. Колебания тока в двухдолинных полупроводниках (эффект Ганна).
- §12. Токи ограниченные пространственным зарядом (ТОПЗ) в полупроводниках без “ловушек”.
- §13. ТОПЗ в полупроводниках с ловушками.
- §14. Основные свойства сверхпроводящего состояния твердых тел.
- §15. Природа сверхпроводимости (теория БКШ).
- §16. Применение сверхпроводимости.
§2. Дрейфовая электропроводность в полупроводнике.
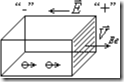 Найдем выражение для дрейфовой электропроводности в полупроводнике. В общем случае имеются два типа носителей заряда. Сначала рассчитаем выражение для дрейфовой плотности электрического тока, вызванного переносом электронов. Для этого рассмотрим полупроводник в виде параллелепипеда с ребром
Найдем выражение для дрейфовой электропроводности в полупроводнике. В общем случае имеются два типа носителей заряда. Сначала рассчитаем выражение для дрейфовой плотности электрического тока, вызванного переносом электронов. Для этого рассмотрим полупроводник в виде параллелепипеда с ребром ![]() и площадью поперечного сечения
и площадью поперечного сечения ![]() . Электрическое поле направлено вдоль ребра, так как показано на рисунке.
. Электрическое поле направлено вдоль ребра, так как показано на рисунке.
![]() — концентрация электронов. Внутри параллелепипеда находится заряд электронов:
— концентрация электронов. Внутри параллелепипеда находится заряд электронов:
За время ![]() все электроны пересекут заштрихованную площадку. Плотность электрического тока будет равна:
все электроны пересекут заштрихованную площадку. Плотность электрического тока будет равна:
В векторном виде:
Дрейфовая плотность дырочного тока равна:
Таким образом, в полупроводнике со смешанной проводимостью дрейфовая плотность тока равна:
Найдем связь дрейфовой скорости носителей заряда с напряженностью электрического поля. Из §1 следует, что:
![]() и
и ![]() — подвижность электронов дырок и соответственно, это скорость направленного движения (скорость дрейфа в единичном электрическом поле).
— подвижность электронов дырок и соответственно, это скорость направленного движения (скорость дрейфа в единичном электрическом поле).
(5) и (6) связывают макроскопические параметры полупроводника (подвижность) с микроскопическими параметрами ![]() . Учитывая (5) и (6) из (3) следует:
. Учитывая (5) и (6) из (3) следует:
В выражении для ![]() знак “+” следует из того, что направление скорости электронов
знак “+” следует из того, что направление скорости электронов ![]() противоположно направлению электрического поля
противоположно направлению электрического поля ![]() . С другой стороны в соответствии с законом Ома:
. С другой стороны в соответствии с законом Ома:
где ![]() — удельная электропроводность, следовательно, из (7) и (8) вытекает, что электропроводность полупроводника, у которого имеются электроны и дырки равна:
— удельная электропроводность, следовательно, из (7) и (8) вытекает, что электропроводность полупроводника, у которого имеются электроны и дырки равна:
В монополярном полупроводнике ![]() — типа концентрация дырок
— типа концентрация дырок ![]()
В монополярном полупроводнике ![]() — типа концентрация электронов
— типа концентрация электронов ![]()
Если полупроводник имеет форму параллелепипеда или цилиндра длиной ![]() и площадью поперечного сечения
и площадью поперечного сечения ![]() , то
, то