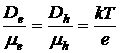Лекции для студентов

Физика полупроводников. Лекция 4

§3. Диффузионная электропроводность в полупроводнике. Соотношения Эйнштейна.

В реальных полупроводниках концентрация носителей заряда электронов и дырок может быть неоднородно распределена по объему. В этом случае вместе с тепловым движением зарядов наблюдается их перенос из одной области полупроводника в другую, за счет диффузии (перенос). Эти условия можно создать, например неоднородным легирование полупроводника мелкой примесью вдоль его длины. Это можно также достичь неоднородным возбуждением вдоль его длины.

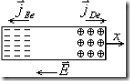
Для определенности рассмотрим монополярный полупроводник  — типа в форме параллелепипеда. Направим ось x вдоль его большого ребра. И пусть полупроводник пролегирован мелкими донорами, неоднородно так, что вдоль оси x имеется положительный градиент концентрации электронов . Концентрация электронов, возрастает слева направо вдоль положительного направления оси x. В этом случае будет иметь место диффузия электронов в направлении справа налево. Диффузионный ток электронов будет направлен, так как показано на рисунке.

В результате диффузии электронов появится объемный заряд положительных ионов доноров в области, где концентрация их была высока и отрицательный заряд электронов в области, где их концентрация была меньше. Появление объемного заряда приводит к появлению электрического поля в направлении как показано на рисунке (хотя внешнее поле может отсутствовать). Очевидно диффузионный ток электронов тем больше чем больше градиент концентрации, его можно представить в виде:

(1)

где  — коэффициент диффузии электронов. Электронный ток направлен в сторону градиента концентрации, поэтому знак “+”. Выражение для дырочного тока диффузии примет вид:

(2)

в (2) знак “-” потому что диффузионный ток направлен противоположно градиенту концентрации дырок. Электрическое поле вызывает дрейфовый ток. Электрическое поле в полупроводнике может быть создано за счет объемного заряда плюс внешнее электрическое поле. Так или иначе, полный ток через полупроводник будет складываться из дрейфового и диффузионного тока. Если полупроводник однородно пролегирован, то диффузионный ток равен нулю.

(3)

(4)

Найдем связь между подвижностью носителей заряда и коэффициентом диффузии. Подвижность описывает дрейф носителей заряда, а и их диффузию. Физическая причина появления этих коэффициентов одинакова, она обусловлена рассеянием носителей заряда. В равновесных условиях . Тогда из (3) следует

(5)

Напряженность электрического поля ,  — потенциал объемного заряда в точке. Тогда энергия электронов в зоне проводимости ,

(5)

В поле объемного заряда края зон и не являются горизонтальными

(6)

(7)

Подставим (7) в (5) и получим

(8)

(9)

(8), (9) — соотношения Эйнштейна. Эти соотношения верны только для невырожденных полупроводников (для равновесного и не равновесного состояния).

(10)

При . Например, коэффициент диффузии в кристаллах кремния , .

Диффузия в металлах крайне не значительна, так как концентрация электронов велика. Однако в полупроводниках концентрацию носителей заряда можно менять в широких приделах.