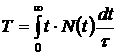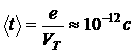Физика полупроводников. Лекция 4
- Физика полупроводников. Лекция 4
- §2. Дрейфовая электропроводность в полупроводнике.
- §3. Диффузионная электропроводность в полупроводнике. Соотношения Эйнштейна.
- §4. Температурная зависимость подвижности носителей заряда в полупроводниках.
- §5. Температурная зависимость подвижности при смешанном механизме рассеяния носителей заряда.
- §6. Разогрев носителей заряда в сильных электрических полях.
- §7. Термоэлектронная ионизация Френкеля.
- §8. Ударная ионизация в полупроводниках.
- §9. Туннельный эффект в полупроводниках (электростатическая ионизация Зинера).
- §10. Отрицательная дифференциальная проводимость (ОДП) полупроводников с двух долинной зонной структурой.
- §11. Колебания тока в двухдолинных полупроводниках (эффект Ганна).
- §12. Токи ограниченные пространственным зарядом (ТОПЗ) в полупроводниках без “ловушек”.
- §13. ТОПЗ в полупроводниках с ловушками.
- §14. Основные свойства сверхпроводящего состояния твердых тел.
- §15. Природа сверхпроводимости (теория БКШ).
- §16. Применение сверхпроводимости.
Глава IV. Элементы теории электропроводности полупроводников.
§1. Представление о рассеянии и дрейфе носителей заряда в полупроводниках.
Явление переноса носителей заряда (зонные электроны и дырки) и тепла под действием внешних сил (электрическое и магнитное поле, градиент температуры и т.п.) называются кинетическими эффектами, к ним относятся явление электропроводности в полупроводнике, перенос носителей заряда под действием электрического поля.
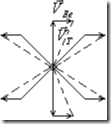 При T > 0 K0 носители зарядов в полупроводниках перемещаются за счет тепловой энергии, т.е. энергии кристаллической решетки, однако в отсутствии внешнего возбуждения такое движение носителей заряда является хаотическим, неупорядоченным. Это связано с тем, что реальные кристаллы имеют разного рода дефекты (колебания решетки, примеси, собственные дефекты и т.д.), которые нарушают идеальность в периодической структуре кристалла. Носители заряда, сталкиваясь с такими дефектами, изменяют направление своего движения, т.е. рассеиваются. В результате этого тепловое движение носителей заряда носит хаотический характер. Среднее значение скорости теплового движения носителей заряда как векторной величины равно нулю. Это означает, что для каждого носителя заряда имеется другой такой же носитель заряда, который движется с такой же скоростью, но в противоположном направлении (смотри рисунок). Следовательно, суммарный заряд, переносимый носителем заряда будет равен нулю, следовательно, тепловое движение электронов не дает электрического тока.
При T > 0 K0 носители зарядов в полупроводниках перемещаются за счет тепловой энергии, т.е. энергии кристаллической решетки, однако в отсутствии внешнего возбуждения такое движение носителей заряда является хаотическим, неупорядоченным. Это связано с тем, что реальные кристаллы имеют разного рода дефекты (колебания решетки, примеси, собственные дефекты и т.д.), которые нарушают идеальность в периодической структуре кристалла. Носители заряда, сталкиваясь с такими дефектами, изменяют направление своего движения, т.е. рассеиваются. В результате этого тепловое движение носителей заряда носит хаотический характер. Среднее значение скорости теплового движения носителей заряда как векторной величины равно нулю. Это означает, что для каждого носителя заряда имеется другой такой же носитель заряда, который движется с такой же скоростью, но в противоположном направлении (смотри рисунок). Следовательно, суммарный заряд, переносимый носителем заряда будет равен нулю, следовательно, тепловое движение электронов не дает электрического тока.
Приложим к кристаллу электрическое поле ![]() , в этом случае носители заряда будут ускорятся под действием силы
, в этом случае носители заряда будут ускорятся под действием силы ![]() и приобретать дополнительную скорость в направлении против электрического поля (в зависимости от знак носителя заряда). В этом случае носители заряда одновременно участвуют как в тепловом движении, так и в упорядоченном движении под действием электрического поля. Будем обозначать скорость электронов и дырок в электрическом поле соответственно через
и приобретать дополнительную скорость в направлении против электрического поля (в зависимости от знак носителя заряда). В этом случае носители заряда одновременно участвуют как в тепловом движении, так и в упорядоченном движении под действием электрического поля. Будем обозначать скорость электронов и дырок в электрическом поле соответственно через ![]() ,
, ![]() . Пунктиром обозначена суммарная скорость
. Пунктиром обозначена суммарная скорость ![]() . Среднее значение суммарных скоростей носителей заряда теперь не будет равно нулю. В данном случае будет наблюдаться направленное движение всей совокупности носителей заряда в направлении или против электрического поля, т.е. через полупроводник будет протекать ток.
. Среднее значение суммарных скоростей носителей заряда теперь не будет равно нулю. В данном случае будет наблюдаться направленное движение всей совокупности носителей заряда в направлении или против электрического поля, т.е. через полупроводник будет протекать ток.
В случае слабых электрических полей характер и темп рассеивания носителей заряда будет таким же, как и до приложения электрического поля ![]() . Энергию, которую приобретают носители заряда в электрическом поле при столкновении с дефектами решетки, они полностью передают ее ей. После этого столкновения носители заряда приходят в состояние теплового равновесия с кристаллической решеткой. В дальнейшем носители заряда снова приобретают в электрическом поле дополнительную энергию и т.д.
. Энергию, которую приобретают носители заряда в электрическом поле при столкновении с дефектами решетки, они полностью передают ее ей. После этого столкновения носители заряда приходят в состояние теплового равновесия с кристаллической решеткой. В дальнейшем носители заряда снова приобретают в электрическом поле дополнительную энергию и т.д.
Направленное движение носителей заряда под действием электрического поля называется дрейфом, а скорость направленного движения в электрическом поле ![]() называется дрейфовой скоростью. Очевидно вероятность столкновения носителей заряда с дефектами решетки, т.е. вероятность рассеивания за время
называется дрейфовой скоростью. Очевидно вероятность столкновения носителей заряда с дефектами решетки, т.е. вероятность рассеивания за время ![]() прямо пропорционально этой величине:
прямо пропорционально этой величине: ![]() . Будем считать, что величина
. Будем считать, что величина ![]() , имеющая размерность времени не зависит от времени, тогда вероятность рассеивания за время
, имеющая размерность времени не зависит от времени, тогда вероятность рассеивания за время ![]()
![]() носителей заряда будет равна:
носителей заряда будет равна: ![]() , отсюда следует, что за время
, отсюда следует, что за время ![]() число носителей заряда, движущихся в данном направлении, уменьшается за счет рассеивания на величину:
число носителей заряда, движущихся в данном направлении, уменьшается за счет рассеивания на величину:
Решением уравнения (1) является:
![]() — число носителей заряда не испытавших рассеивание к моменту времени t.
— число носителей заряда не испытавших рассеивание к моменту времени t.
Видно, что число нерассеваемых носителей заряда уменьшается со временем по закону ![]() ,
, ![]() — время релаксации, численно равно времени t за которое
— время релаксации, численно равно времени t за которое ![]() уменьшится в e раз. Найдем связь между среднем временем свободного побега t носителей заряда и постоянной времени
уменьшится в e раз. Найдем связь между среднем временем свободного побега t носителей заряда и постоянной времени ![]() . Для этого направим ось x вдоль направления электрического поля. Представим себе, что в момент времени t = 0 все носители испытали рассеивание.
. Для этого направим ось x вдоль направления электрического поля. Представим себе, что в момент времени t = 0 все носители испытали рассеивание. ![]() — времена свободного пробега носителей заряда. Пусть каждый носитель пройдет до следующего столкновения
— времена свободного пробега носителей заряда. Пусть каждый носитель пройдет до следующего столкновения ![]() длины свободного пробега. Носители заряда обозначим через
длины свободного пробега. Носители заряда обозначим через ![]() , очевидно
, очевидно ![]() . Но среди носителей
. Но среди носителей ![]() имеются такие, которые имеют одинаковые времена свободного пробега, например t. Очевидно, эти носители заряда должны испытать рассеивание за время от t до t + dt. Обозначим через
имеются такие, которые имеют одинаковые времена свободного пробега, например t. Очевидно, эти носители заряда должны испытать рассеивание за время от t до t + dt. Обозначим через ![]() число носителей имеющих время свободного пробега t. Число носителей
число носителей имеющих время свободного пробега t. Число носителей ![]() значит эти носители внесут вклад величиной
значит эти носители внесут вклад величиной ![]() в суммарное время T. Отсюда величину T можно получить интегрированием по t величины
в суммарное время T. Отсюда величину T можно получить интегрированием по t величины ![]()
Из (4) следует, что среднее время свободного пробега в полупроводнике равна постоянной ![]() .
.
В сильных электрических полях, когда ![]() сопоставимо с
сопоставимо с ![]() , тогда
, тогда 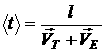 .
.
- Prev
- Вперёд >>